【题目】如图,直角三角板![]() 放在平面直角坐标系中,直角边
放在平面直角坐标系中,直角边![]() 垂直
垂直![]() 轴,垂足为
轴,垂足为![]() ,已知
,已知![]() ,点
,点![]() ,
,![]() ,
,![]() 均在反比例函数
均在反比例函数![]() 的图象上,分别作
的图象上,分别作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,且点
,且点![]() 为
为![]() 的中点.
的中点.

![]() 求点
求点![]() 的坐标;
的坐标;
![]() 求四边形
求四边形![]() 的面积.
的面积.
参考答案:
【答案】(1)点![]() 的坐标是
的坐标是![]() ;(2)
;(2)![]() .
.
【解析】
①因为![]() ,设点
,设点![]() ,根据反比例函数解析式可得出A,C,B的坐标;
,根据反比例函数解析式可得出A,C,B的坐标;
②由点A的坐标可得出EF,AQ的长度,又点![]() 为
为![]() 的中点,所以PF=
的中点,所以PF=![]() ,设点P坐标,因为P在图像上,所以可得出△OPF面积,同理得出△AOD的面积,四边形AOPE的面积=
,设点P坐标,因为P在图像上,所以可得出△OPF面积,同理得出△AOD的面积,四边形AOPE的面积=![]() ,即可得出答案.
,即可得出答案.
解:![]() ∵
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设点![]() ,
,
则 ,
,
解得:![]() 或
或![]() (不合题意,舍去)
(不合题意,舍去)
∴点![]() 的坐标是
的坐标是![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
∴点![]() 的坐标是
的坐标是![]()
![]() ∵点
∵点![]() 的坐标是
的坐标是![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
设点![]() 的坐标是
的坐标是![]() ,则
,则![]()
∵点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-3,2),B(-4,-3),C(-1,-1)。

(1)写出△ABC关于x轴对称的△A1B1C1 的各顶点坐标;
(2)画出△ABC关于y轴对称的△A2B2C2;
(3)求△A2B2C2的面积。
-
科目: 来源: 题型:
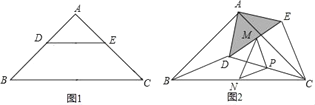
查看答案和解析>>【题目】如图1,在△ABC中,点DE分别在AB、AC上,DE∥BC,BD=CE,
(1)求证:∠B=∠C,AD=AE;
(2)若∠BAC=90°,把△ADE绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.
①判断△PMN的形状,并说明理由;
②把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN的最大面积为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形
 的顶点
的顶点 与原点
与原点 重合,点
重合,点 在
在 轴的
轴的正半轴上,点
 在反比例函数
在反比例函数 的图象上,点
的图象上,点 的坐标为
的坐标为 .
.
 求
求 的值.
的值. 若将菱形
若将菱形 向右平移,使点
向右平移,使点 落在反比例函数
落在反比例函数 的图象上,求菱形
的图象上,求菱形 平移的距离.
平移的距离. 怎样平移可以使点
怎样平移可以使点 、
、 同时落在第一象限的曲线上?
同时落在第一象限的曲线上? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为
 、
、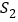 、
、 ,若AD=2,AB=
,若AD=2,AB= ,∠A=60°,则
,∠A=60°,则 的值为( )
的值为( )
A.
 B.
B.  C.
C.  D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C、D是矩形的四个顶点,AB=16cm,BC=6cm,动点P从点A出发,以3cm/s的速度向点B运动,直到点B为止;动点Q同时从点C出发,以2cm/s的速度向点D运动,当时间为_______时,点P和点Q之间的距离是10cm

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A(2,0),点B (0,1),过点A的直线l垂直于线段AB,点P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折
 ,使点C落在点D处,若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为___________________________.
,使点C落在点D处,若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为___________________________.
相关试题

