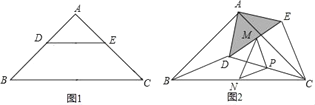
【题目】如图1,在△ABC中,点DE分别在AB、AC上,DE∥BC,BD=CE,
(1)求证:∠B=∠C,AD=AE;
(2)若∠BAC=90°,把△ADE绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.
①判断△PMN的形状,并说明理由;
②把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN的最大面积为
参考答案:
【答案】(1)见解析 (2)①△PMN是等腰直角三角形 ②![]()
【解析】
(1)利用平行线分线段成比例定理得出比例式即可得出AB=AC,即可得出结论;
(2)①利用三角形中位线定理和BD=CE,判断出PM=PN,即:△PMN是等腰三角形,再判断出∠MPN=90°,得出△PMN是等腰直角三角形;
②先判断出PM最大时,△PMN面积最大,即:点D在AB的延长线上,进而求出BD=AB+AD=14,即可得出PM的最大值即可.
(1)∵DE∥BC,∴![]() ,∵BD=CE,∴AB=AC,∴∠B=∠C,
,∵BD=CE,∴AB=AC,∴∠B=∠C,
AB﹣BD=AC﹣CD,∴AD=AE,即:∠B=∠C,AD=AE
(2)①△PMN是等腰直角三角形,理由:∵点P,M分别是CD,DE的中点,∴PM=![]() CE,PM∥CE,
CE,PM∥CE,
∵点N,M分别是BC,DE的中点,∴PN=![]() BD,PN∥BD,∵BD=CE,∴PM=PN,∴△PMN是等腰三角形,∵PM∥CE,∴∠DPM=∠DCE,∵PN∥BD,∴∠PNC=∠DBC,∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
BD,PN∥BD,∵BD=CE,∴PM=PN,∴△PMN是等腰三角形,∵PM∥CE,∴∠DPM=∠DCE,∵PN∥BD,∴∠PNC=∠DBC,∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=90°,∴∠ACB+∠ABC=90°,∴∠MPN=90°,∴△PMN是等腰直角三角形
②由①知,△PMN是等腰直角三角形,PM=PN=![]() BD,∴PM最大时,△PMN面积最大,∴点D在AB的延长线上,∴BD=AB+AD=14,∴PM=7,∴S△PMN最大=
BD,∴PM最大时,△PMN面积最大,∴点D在AB的延长线上,∴BD=AB+AD=14,∴PM=7,∴S△PMN最大=![]() PM2=
PM2=![]() ×72=
×72=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推进垃圾分类,推动绿色发展,某工厂购进甲、乙两种型号的机器人用来进行垃圾分类,甲型机器人比乙型机器人每小时多分20kg,甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等。
(1)两种机器人每小时分别分类多少垃圾?
(2)现在两种机器人共同分类700kg垃圾,工作2小时后甲型机器人因机器维修退出,求甲型机器人退出后乙型机器人还需工作多长时间才能完成?
-
科目: 来源: 题型:
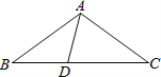
查看答案和解析>>【题目】如图,在△ ABC中,AB=AC,点D在线段BC上,AD=BD,△ ADC是等腰三角形,求△ABC三个内角的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-3,2),B(-4,-3),C(-1,-1)。

(1)写出△ABC关于x轴对称的△A1B1C1 的各顶点坐标;
(2)画出△ABC关于y轴对称的△A2B2C2;
(3)求△A2B2C2的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形
 的顶点
的顶点 与原点
与原点 重合,点
重合,点 在
在 轴的
轴的正半轴上,点
 在反比例函数
在反比例函数 的图象上,点
的图象上,点 的坐标为
的坐标为 .
.
 求
求 的值.
的值. 若将菱形
若将菱形 向右平移,使点
向右平移,使点 落在反比例函数
落在反比例函数 的图象上,求菱形
的图象上,求菱形 平移的距离.
平移的距离.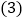 怎样平移可以使点
怎样平移可以使点 、
、 同时落在第一象限的曲线上?
同时落在第一象限的曲线上? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角板
 放在平面直角坐标系中,直角边
放在平面直角坐标系中,直角边 垂直
垂直 轴,垂足为
轴,垂足为 ,已知
,已知 ,点
,点 ,
, ,
, 均在反比例函数
均在反比例函数 的图象上,分别作
的图象上,分别作 轴于
轴于 ,
, 轴于
轴于 ,延长
,延长 ,
, 交于点
交于点 ,且点
,且点 为
为 的中点.
的中点.
 求点
求点 的坐标;
的坐标; 求四边形
求四边形 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为
 、
、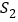 、
、 ,若AD=2,AB=
,若AD=2,AB= ,∠A=60°,则
,∠A=60°,则 的值为( )
的值为( )
A.
 B.
B.  C.
C.  D. 4
D. 4
相关试题

