【题目】对于平面直角坐标系xOy中的点P,Q,给出如下定义:若P,Q为某个三角形的顶点,且边PQ上的高h,满足h=PQ,则称该三角形为点P,Q的“生成三角形”.
(1)已知点A(4,0);
①若以线段OA为底的某等腰三角形恰好是点O,A的“生成三角形”,求该三角形的腰长;
②若Rt△ABC是点A,B的“生成三角形”,且点B在x轴上,点C在直线y=2x﹣5上,则点B的坐标为 ;
(2)⊙T的圆心为点T(2,0),半径为2,点M的坐标为(2,6),N为直线y=x+4上一点,若存在Rt△MND,是点M,N的“生成三角形”,且边ND与⊙T有公共点,直接写出点N的横坐标![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)①![]() ;②(1,0),(3,0)或(7,0);(2)点N的横坐标
;②(1,0),(3,0)或(7,0);(2)点N的横坐标![]() 的取值范围为
的取值范围为![]() .
.
【解析】
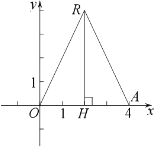
(1)①如图(见解析),设满足条件的三角形为等腰![]() ,过点R作
,过点R作![]() 于点H,由等腰三角形的性质得
于点H,由等腰三角形的性质得![]() ,再根据“生成三角形”的定义可得
,再根据“生成三角形”的定义可得![]() ,最后利用勾股定理即可得;
,最后利用勾股定理即可得;
②依题意,按点![]() 分别为直角顶点三种情况讨论,根据“生成三角形”的定义和直线
分别为直角顶点三种情况讨论,根据“生成三角形”的定义和直线![]() 的解析式分别建立等式,求解即可;
的解析式分别建立等式,求解即可;
(2)根据点![]() 分别为直角顶点三种情况讨论,根据“生成三角形”的定义、结合圆的切线性质列出等式,求解即可.
分别为直角顶点三种情况讨论,根据“生成三角形”的定义、结合圆的切线性质列出等式,求解即可.
(1)①如图,设满足条件的三角形为等腰![]() ,则
,则![]()
过点R作![]() 于点H
于点H
![]()
∵以线段OA为底的等腰![]() 恰好是点O,A的“生成三角形”
恰好是点O,A的“生成三角形”
![]()
在![]() 中,利用勾股定理得:
中,利用勾股定理得:![]()
故该三角形的腰长为![]() ;
;
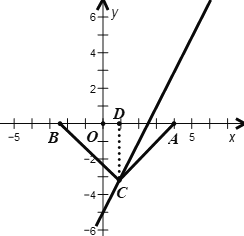
②依题意,分以下三种情况讨论:
当A为直角顶点时,则![]()
因点A的坐标为![]()
令![]() 代入
代入![]() 得
得![]() ,即
,即![]()
设点B的坐标为![]()
则![]() ,解得
,解得![]() 或
或![]()
故点B的坐标为![]() 或
或![]()
当B为直角顶点时,则![]()
设点B的坐标为![]() ,则
,则![]()
令![]() 代入
代入![]() 得
得![]() ,即
,即![]()
则有![]()
两边平方化简得![]() ,解得
,解得![]() 或
或![]()
故点B的坐标为![]() 或
或![]()
当C为直角顶点时,如图,过点C作![]() 于点D
于点D
设点D的坐标为![]() ,则
,则![]()
令![]() 代入
代入![]() 得
得![]()
由“生成三角形”的定义得![]()
则![]()
![]()
![]()
又![]()
![]()
![]() ,即
,即![]()
令![]() ,则
,则![]()
化简得![]() ,此方程的根的判别式
,此方程的根的判别式![]() ,方程没有实数根
,方程没有实数根
则点C不能为![]() 的直角顶点
的直角顶点
综上,点B的坐标为![]() ,
,![]() 或
或![]() ;
;
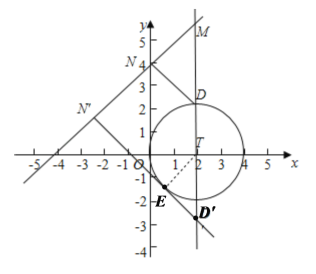
(2)当N为直角顶点时
由点M的坐标![]() 可知,点M在直线
可知,点M在直线![]() 上
上
由直线![]() 可知,
可知,![]()
则当点D在MT所在直线![]() 时,
时,![]() 是点M,N的“生成三角形”
是点M,N的“生成三角形”
如图,点N和![]() 是符合条件的两个临界位置
是符合条件的两个临界位置
由图可知,点D的坐标为![]() ,
,![]()
在![]() 中,
中,![]()
设点N的坐标为![]()
由两点之间距离公式得![]()
解得![]() ,再代入直线
,再代入直线![]() 得
得![]()
当点N在![]() 处时,图中
处时,图中![]() 也是符合条件的“生成三角形”
也是符合条件的“生成三角形”
此时,![]() 恰好与圆T相切,半径
恰好与圆T相切,半径![]()
则![]() 是等腰直角三角形,且
是等腰直角三角形,且![]()
![]()
则点![]() 的坐标为
的坐标为![]() ,设点
,设点![]() 的坐标为
的坐标为![]()
由两点之间距离公式得![]()
解得![]() ,再代入直线
,再代入直线![]() 得
得![]()
故当点N为直角顶点时,点N的横坐标![]() 的取值范围为
的取值范围为![]()
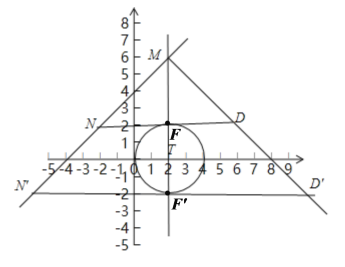
当点M为直角顶点时,![]()
如图,![]() 和
和![]() 均平行于x轴,且与圆T分别相切于点F,
均平行于x轴,且与圆T分别相切于点F,![]()
由平行线的性质和直线![]() 可知,
可知,![]()
则![]() 和
和![]() 都是等腰直角三角形
都是等腰直角三角形
因此,![]() 和
和![]() 都是符合条件的“生成三角形”, 此时,点N和
都是符合条件的“生成三角形”, 此时,点N和![]() 是符合条件的两个临界位置
是符合条件的两个临界位置
设点N的坐标为![]()
![]() 点F的坐标为
点F的坐标为![]()
![]() 点N的纵坐标为2,即
点N的纵坐标为2,即![]()
将![]() 代入
代入![]() 得
得![]()
同理可得![]()
故当点M为直角顶点时,点N的横坐标![]() 的取值范围为
的取值范围为![]()
当点D为直角顶点时,同(1)②中,当C为直角顶点时的思路一样,可证此时不存在符合条件的![]()
综上,点N的横坐标![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是直径AB上的一点,AB=6,CP⊥AB交半圆
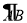 于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
小明根据学习函数的经验,对线段AP,BC,OD的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,BC,OD的长度的几组值,如下表:
位置1
位置2
位置3
位置4
位置5
位置6
位置…
AP
0.00
1.00
2.00
3.00
4.00
5.00
…
BC
6.00
5.48
4.90
4.24
3.46
2.45
…
OD
6.71
7.24
7.07
6.71
6.16
5.33
…
在AP,BC,OD的长度这三个量中,确定________的长度是自变量,________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;

(3)结合函数图象,解决问题:当OD=2BC时,线段AP的长度约为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣6mx+9m+1(m≠0).
(1)求抛物线的顶点坐标;
(2)若抛物线与x轴的两个交点分别为A和B点(点A在点B的左侧),且AB=4,求m的值.
(3)已知四个点C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若抛物线与线段CD和线段EF都没有公共点,请直接写出m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角∠AOB如图,
(1)在射线OA上取一点C,以点O为圆心,OC长为半径作弧DE,交射线OB于点F,连接CF;
(2)以点F为圆心,CF长为半径作弧,交弧DE于点G;
(3)连接FG,CG.作射线OG.
根据以上作图过程及所作图形,下列结论中错误的是( )
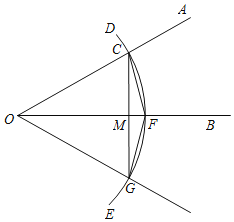
A.∠BOG=∠AOBB.若CG=OC,则∠AOB=30°
C.OF垂直平分CGD.CG=2FG
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在“爱护地球,绿化祖国”的活动中,组织同学开展植树造林活动,为了了解同学的植树情况,学校抽查了初一年级所有同学的植树情况(初一年级共有两个班),并将调查数据整理绘制成如下所示的部分数据尚不完整的统计图表.下面有四个推断:
初一年级植树情况统计表
棵树/棵
1
2
3
4
5
人数
7
33
a
12
3
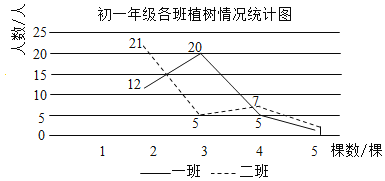
①a的值为20;
②初一年级共有80人;
③一班植树棵树的众数是3;
④二班植树棵树的是中位数2.
其中合理的是( )
A.①③B.②④C.②③D.②③④
-
科目: 来源: 题型:
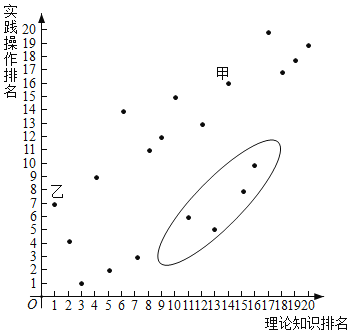
查看答案和解析>>【题目】某公司计划招募10名技术人员,他们对20名面试合格人员进行了测试,测试包括理论知识和实践操作两部分,20名应聘者的成绩排名情况如图所示,下面有3个推断:
①甲测试成绩非常优秀,入选的可能性很大;
②乙的理论知识排名比实践操作排名靠前;
③位于椭圆形区域内的应聘者应该加强该专业理论知识的学习;
其中合理的是_____.(写序号)
相关试题

