【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣6mx+9m+1(m≠0).
(1)求抛物线的顶点坐标;
(2)若抛物线与x轴的两个交点分别为A和B点(点A在点B的左侧),且AB=4,求m的值.
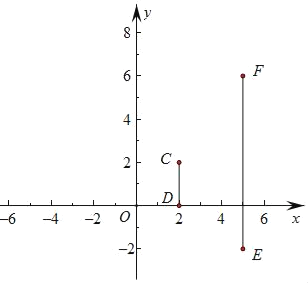
(3)已知四个点C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若抛物线与线段CD和线段EF都没有公共点,请直接写出m的取值范围.
参考答案:
【答案】(1)顶点坐标为(3,1);(2)m=﹣![]() ;(3)m<﹣1或m>
;(3)m<﹣1或m>![]() .
.
【解析】
(1)利用配方法得y═m(x﹣3)2+1,由此即可得出顶点坐标;
(2)根据抛物线的对称轴以及AB=4,即可得到A、B两点的坐标,代入抛物线即可求出m的值;
(3)结合图象即可得出当抛物线与线段CD和线段EF都没有公共点时m的取值范围.
(1)∵y=mx2﹣6mx+9m+1=m(x﹣3)2+1,
∴抛物线的顶点坐标为(3,1);
(2)∵对称轴为直线x=3,且AB=4,
∴A(1,0),B(5,0),
将点A的坐标代入抛物线,可得:m=﹣![]() ;
;
(3)如图:
①当m>0时满足![]() ,解得:m>
,解得:m>![]() ;
;
②当m<时满足![]() ,解得:m<﹣1;
,解得:m<﹣1;
综上,m<﹣1或m>![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系
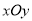 中的点
中的点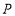 ,
,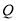 ,给出如下定义:若
,给出如下定义:若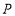 ,
,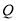 为某个三角形的顶点,且边
为某个三角形的顶点,且边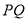 上的高
上的高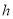 ,满足
,满足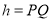 ,则称该三角形为点
,则称该三角形为点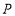 ,
,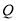 的“生成三角形”.
的“生成三角形”.(1)已知点
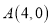 ;
;①若以线段
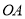 为底的某等腰三角形恰好是点
为底的某等腰三角形恰好是点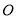 ,
,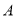 的“生成三角形”,求该三角形的腰长;
的“生成三角形”,求该三角形的腰长;②若
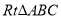 是点
是点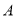 ,
,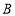 的“生成三角形”,且点
的“生成三角形”,且点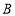 在
在 轴上,点
轴上,点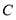 在直线
在直线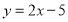 上,则点
上,则点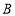 的坐标为______;
的坐标为______;(2)
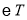 的圆心为点
的圆心为点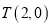 ,半径为2,点
,半径为2,点 的坐标为
的坐标为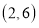 ,
,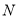 为直线
为直线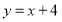 上一点,若存在
上一点,若存在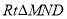 ,是点
,是点 ,
,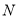 的“生成三角形”,且边
的“生成三角形”,且边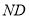 与
与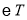 有公共点,直接写出点
有公共点,直接写出点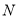 的横坐标
的横坐标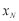 的取值范围.
的取值范围. -
科目: 来源: 题型:
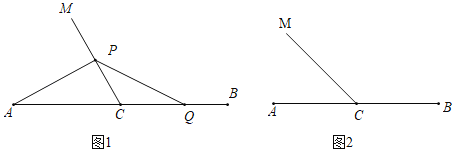
查看答案和解析>>【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是直径AB上的一点,AB=6,CP⊥AB交半圆
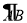 于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
小明根据学习函数的经验,对线段AP,BC,OD的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,BC,OD的长度的几组值,如下表:
位置1
位置2
位置3
位置4
位置5
位置6
位置…
AP
0.00
1.00
2.00
3.00
4.00
5.00
…
BC
6.00
5.48
4.90
4.24
3.46
2.45
…
OD
6.71
7.24
7.07
6.71
6.16
5.33
…
在AP,BC,OD的长度这三个量中,确定________的长度是自变量,________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;

(3)结合函数图象,解决问题:当OD=2BC时,线段AP的长度约为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了推动全社会自觉尊法学法守法用法,促进全面依法治国,某区每年都举办普法知识竞赛,该区某单位甲、乙两个部门各有员工200人,要在这两个部门中挑选一个部门代表单位参加今年的竞赛,为了解这两个部门员工对法律知识的掌握情况,进行了抽样调查,从甲、乙两个部门各随机抽取20名员工,进行了法律知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理,描述和分析,下面给出了部分信息.
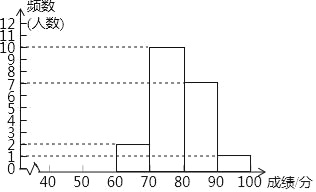
a.甲部门成绩的频数分布直方图如下(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100)
b.乙部门成绩如下:
40 52 70 70 71 73 77 78 80 81
82 82 82 82 83 83 83 86 91 94
c.甲、乙两部门成绩的平均数、方差、中位数如下:
平均数
方差
中位数
甲
79.6
36.84
78.5
乙
77
147.2
m
d.近五年该单位参赛员工进入复赛的出线成绩如下:
2014年
2015年
2016年
2017年
2018年
出线成绩(百分制)
79
81
80
81
82
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)可以推断出选择 部门参赛更好,理由为 ;
(3)预估(2)中部门今年参赛进入复赛的人数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线l:y=x+b与x轴交于点A(﹣2,0),与y轴交于点B.双曲线y
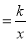 与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标
与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标(1)求点B的坐标;
(2)当点P的横坐标为2时,求k的值;
(3)连接PO,记△POB的面积为S.若
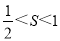 ,结合函数图象,直接写出k的取值范围.
,结合函数图象,直接写出k的取值范围.
相关试题

