【题目】如图,等腰△ABC中,AB=AC,∠ABC=35°,E是BC边上一点且AE=CE,D是
BC边上的中点,连接AD,AE.
(1)求∠DAE的度数;
(2)若BD上存在点F,且∠AFE=∠AEF,求证:BF=CE.

参考答案:
【答案】(1)∠DAE=20°;(2)见解析
【解析】
(1)根据等边对等角和已知∠ABC的度数可求得∠CAE的度数,再根据等腰三角形三线合一的性质可得AD⊥BC,然后根据直角三角形的性质可求出∠DAC的度数,进一步即可求出结果;
(2)先根据等角对等边得到AF=AE,再根据等腰三角形三线合一的性质得FD=ED,进一步即得结论.
解:(1)∵AB=AC,∠ABC=35°,∴∠C=35°,
∵AE=CE,∴∠CAE=∠C=35°,
∵D是BC边上的中点,∴AD⊥BC,∴∠ADC=90°,
∴∠DAC=90°﹣35°=55°,
∴∠DAE=∠DAC﹣∠CAE=55°﹣35°=20°;
(2)证明:∵∠AFE=∠AEF,∴AF=AE,
∵AD⊥BC,∴D是EF边上的中点,∴FD=ED,
∵D是BC边上的中点,∴BD=CD,
∴BD﹣FD=CD﹣ED,即BF=CE.
-
科目: 来源: 题型:
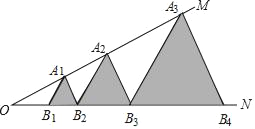
查看答案和解析>>【题目】如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1B2、△A2B2B3、△A3B3B4、…均为等边三角形,若OB1=1,则△A8B8B9的边长为_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的坐标系中,△ABC的三个顶点的坐标依次为A(﹣1,2),B(﹣4,1),C(﹣2,﹣2)
(1)请写出△ABC关于x轴对称的点A1、B1、C1的坐标;
(2)请在这个坐标系中作出△ABC关于y轴对称的△A2B2C2;
(3)计算:△A2B2C2的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的解题过程,再解决问题.
解方程: x4 -6x2 +5=0.
这是一个一元四次方程,根据该方程的特点,它的通常解法是:
设 x2 = y ,则原方程可化为 y2 -6y+5=0.①
解这个方程,得 y1 =1, y2 =5.当 y =1时, x=±1;当 y=5时, x=±
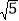 .所以原方程有四个根: x1 =1, x2 =-1, x3 =
.所以原方程有四个根: x1 =1, x2 =-1, x3 =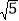 , x4 =-
, x4 =-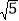 .
. (1)填空:在由原方程得到方程①的过程中,利用________法达到降次的目的,体现了________的数学思想.
(2)解方程:( x2 -x )2 -4(x2 -x )-12=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的部分图象如图所示,则关于
的部分图象如图所示,则关于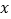 的一元二次方程
的一元二次方程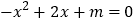 的解为 .
的解为 .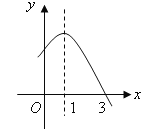
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从百货大楼出发负责送货,向东走了2千米到达小明家,继续向东走了4千米到达小红家,然后向西走了9千米到达小刚家,最后返回百货大楼.
(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置;
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油0.5升,那么这辆货车共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上每相邻两点相距一个单位长度,点A、B、C、D是这些点中的四个,且对应的位置如图所示,它们对应的数分别是a、b、c、d.

(1)若c与d互为相反数,则a________;
(2)若d2b8,那么点C对应的数是________;
(3)若abcd0,ab0求
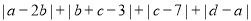 的取值范围.
的取值范围.
相关试题

