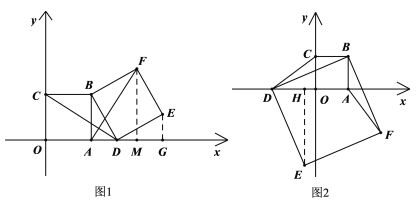
【题目】在平面直角坐标系中,已知A(3,0),以OA为一边在第一象限内画正方形OABC,D(m,0)为x轴上的一个动点,以BD为一边画正方形BDEF(点F在直线AB右侧).
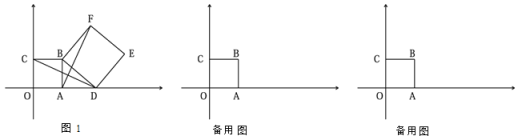
(1)当m>3时(如图1),试判断线段AF与CD的数量关系,并说明理由.
(2)当AF=5时,求点E的坐标;
(3)当D点从A点向右移动4个单位,求这一过程中F点移动的路程是多少?
参考答案:
【答案】(1)![]() ,理由见解析;(2)点E的坐标为
,理由见解析;(2)点E的坐标为![]() 或
或![]() ;(3)这一过程中F点移动的路程是向上移动4个单位.
;(3)这一过程中F点移动的路程是向上移动4个单位.
【解析】
(1)先根据正方形的性质得出![]() ,再根据角的和差求出
,再根据角的和差求出![]() ,然后根据三角形全等的判定定理与性质即可得;
,然后根据三角形全等的判定定理与性质即可得;
(2)分点D在点A的右侧和点D在点A的左侧,分别画出图形.①如图1,先利用(1)的结论可得![]() ,再利用勾股定理求出
,再利用勾股定理求出![]() ,从而可得
,从而可得![]() ,然后过点E作
,然后过点E作![]() 轴于点G,根据三角形全等的判定定理与性质可得
轴于点G,根据三角形全等的判定定理与性质可得![]() ,从而可得
,从而可得![]() ,由此即可得;②如图2,同①的方法,利用三角形全等的判定定理与性质得出
,由此即可得;②如图2,同①的方法,利用三角形全等的判定定理与性质得出![]() ,从而可得
,从而可得![]() ,由此即可得;
,由此即可得;
(3)参照(2)①的方法,求出点F的坐标,从中可发现点F的坐标与m的关系,由此即可得出答案.
(1)![]() ,理由如下:
,理由如下:
![]() 四边形OABC和四边形BDEF都是正方形
四边形OABC和四边形BDEF都是正方形
![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,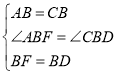
![]()
![]() ;
;
(2)由题意,分以下两种情况:
①如图1,点D在点A的右侧
![]() 四边形OABC和四边形BDEF都是正方形,
四边形OABC和四边形BDEF都是正方形,![]()
![]() ,
,![]() ,
,![]()
![]() ,即
,即![]()
由(1)可知,![]()
在![]() 中,
中,![]()
![]()
过点E作![]() 轴于点G
轴于点G
在![]() 和
和![]() 中,
中,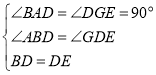
![]()
![]()
![]()
此时点E的坐标为![]()
②如图2,点D在点A的左侧
由(1)可知,![]()
在![]() 中,
中,![]()
![]()
过点E作![]() 轴于点H
轴于点H
同理可证:![]()
![]()
![]()
此时点E的坐标为![]()
综上,点E的坐标为![]() 或
或![]() ;
;
(3)由题意,只需求出点D在点A的右侧,即![]() 时,点F的坐标即可解决问题
时,点F的坐标即可解决问题
如图1,过点F作![]() 轴于点M
轴于点M
由(1)已证:![]()
![]() ,
,![]()
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,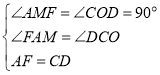
![]()
![]()
![]()
此时点F的坐标为![]()
由此可知,当D点从A点向右移动4个单位时,点F向上移动4个单位
即这一过程中F点移动的路程是向上移动4个单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=4,将纸片折叠,使顶点B落在边AD上的点为E,折痕的一端G点在BC上(BG<GC),另一端F落在矩形的边上,BG=5.
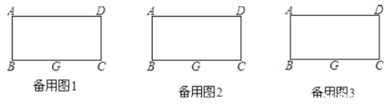
(1)请你在备用图中画出满足条件的图形;
(2)求出AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1.将三角板中30°角的顶点D放在AB边上移动,使这个30°角的两边分别与△ABC的边AC,BC相交于点E,F,且使DE始终与AB垂直.

(1)△BDF是什么三角形?请说明理由;
(2)设AD=x,CF=y,试求y与x之间的函数关系式;(不用写出自变量x的取值范围)
(3)当移动点D使EF∥AB时,求AD的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x与反比例函数y=
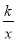 (k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图象上任意一点(不与点A重合),BC⊥x轴于点C.
(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图象上任意一点(不与点A重合),BC⊥x轴于点C.(1)求k的值;
(2)求△OBC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我校开展的社团活动有:A.动漫社团;B.轮滑社团:C.音乐社团;D.诗歌社团;E.书法社团.学生管理中心为了了解全校500名学生的社团需求,开展了一次调查研究,请将下面的调查过程补全
抽样调查:从七、八、九三个年级中随机抽取男女生各20名进行问卷调研;
收集数据:抽样方法确定后,学生管理中心收集到如下数据(社团项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B
A,C,E,D,B,A,B,E,C,A
D,D,B,B,C,C,A,A,E,B
C,B,D,C,A,C,C,A,C,E
整理、描述数据:划记、整理、描述样本数据、绘制统计图如下,请补全统计表和统计图
社团项目
划记
人数
A动漫社

8
B轮滑社
C音乐社
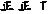
12
D诗歌社
E书法社
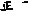
6
合计
40
40
分析数据、推断结论

(1)在扇形统计图中,“B轮滑社团”所在的扇形的圆心角等于 度;
(2)根据学生管理中心获得的样本数据,估计全校大约有 名同学选择D社团.
-
科目: 来源: 题型:
查看答案和解析>>【题目】能判定四边形
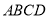 是平行四边形的是( )
是平行四边形的是( )A.AB∥CD,
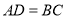 B. AB∥CD,
B. AB∥CD,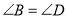
C.
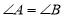 ,
,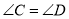 D.
D.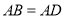 ,
,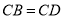
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣4,0)、B(﹣3,﹣3)、C(0,﹣5)
(1)画出△ABC;
(2)△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+5,y1+3).画出平移后的△A′B′C′,并求△A′B′C′的面积;
(3)设直线A′C′与x轴交于点Q,求交点Q坐标.
相关试题

