【题目】如图,矩形纸片ABCD中,AB=4,将纸片折叠,使顶点B落在边AD上的点为E,折痕的一端G点在BC上(BG<GC),另一端F落在矩形的边上,BG=5.
(1)请你在备用图中画出满足条件的图形;
(2)求出AF的长.
参考答案:
【答案】(1)图见解析;(2)AF的长为![]() 或3.
或3.
【解析】
(1)根据折叠的性质和顶点B折叠后的落点可确定另一端F的位置,由此画图即可得;
(2)在图1中,过点G 作![]() 于点M,先根据矩形的性质、折叠的性质得出
于点M,先根据矩形的性质、折叠的性质得出![]() ,
,![]() ,
,![]() ,再利用勾股定理可得EM的长,从而可得AE的长,设
,再利用勾股定理可得EM的长,从而可得AE的长,设![]() ,然后在
,然后在![]() 中,利用勾股定理即可得;在图2中,过点G 作
中,利用勾股定理即可得;在图2中,过点G 作![]() 于点N,先根据线段的和差求出FN的长,再利用勾股定理求出EN的长,从而可得EF的长,然后在
于点N,先根据线段的和差求出FN的长,再利用勾股定理求出EN的长,从而可得EF的长,然后在![]() 中,利用勾股定理即可得.
中,利用勾股定理即可得.
(1)根据折叠的性质和顶点B折叠后的落点,可分以下两种情况:
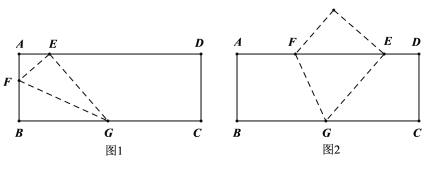
①当另一端F落在矩形的边AB上时,作图结果如图1所示:
②当另一端F落在矩形的边AD上时,作图结果如图2所示:
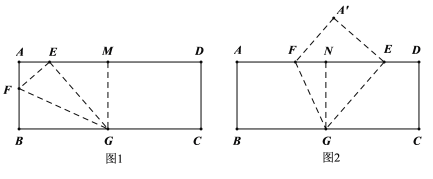
(2)①在图1中,过点G 作![]() 于点M,则四边形ABGM是矩形
于点M,则四边形ABGM是矩形
![]() ,
,![]()
由折叠的性质得:![]() ,
,![]()
在![]() 中,
中,![]()
![]()
![]() 四边形ABCD是矩形
四边形ABCD是矩形
![]()
设![]() ,则
,则![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
②在图2中,过点G 作![]() 于点N,则四边形ABGN是矩形
于点N,则四边形ABGN是矩形
![]() ,
,![]()
由折叠的性质得:![]() ,
,![]() ,
,![]() ,
,![]()
![]()
在![]() 中,
中,![]()
设![]() ,则
,则![]() ,
,![]()
![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
综上,AF的长为![]() 或3.
或3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形。
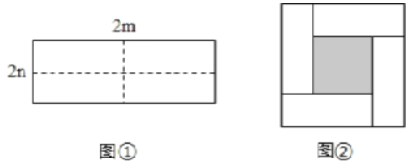
(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一:
 ;
;方法二:
 .
.(2)(m+n)
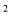 ,(mn)
,(mn) 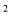 ,mn这三个代数式之间的等量关系为___
,mn这三个代数式之间的等量关系为___(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求xy的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司经销甲种型号电脑,受疫情影响,电脑价格不断下降,今年四月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的甲种电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年四月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再进销售价为6000元的乙种型号电脑,四月份甲、乙两种电脑共销售15台,如果销售额不低于8万元,则乙种型号电脑销售不低于多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个汽车零件制造车间可以生产甲,乙两种零件,生产4个甲种零件和3个乙种零件共获利120元;生产2个甲种零件和5个乙种零件共获利130元.
(1)求生产1个甲种零件,1个乙种零件分别获利多少元?
(2)若该汽车零件制造车间共有工人30名,每名工人每天可生产甲种零件6个或乙种零件5个,每名工人每天只能生产同一种零件,要使该车间每天生产的两种零件所获总利润超过2800元,至少要派多少名工人去生产乙种零件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1.将三角板中30°角的顶点D放在AB边上移动,使这个30°角的两边分别与△ABC的边AC,BC相交于点E,F,且使DE始终与AB垂直.

(1)△BDF是什么三角形?请说明理由;
(2)设AD=x,CF=y,试求y与x之间的函数关系式;(不用写出自变量x的取值范围)
(3)当移动点D使EF∥AB时,求AD的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x与反比例函数y=
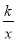 (k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图象上任意一点(不与点A重合),BC⊥x轴于点C.
(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图象上任意一点(不与点A重合),BC⊥x轴于点C.(1)求k的值;
(2)求△OBC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知A(3,0),以OA为一边在第一象限内画正方形OABC,D(m,0)为x轴上的一个动点,以BD为一边画正方形BDEF(点F在直线AB右侧).
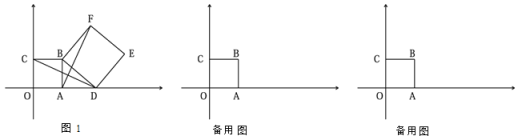
(1)当m>3时(如图1),试判断线段AF与CD的数量关系,并说明理由.
(2)当AF=5时,求点E的坐标;
(3)当D点从A点向右移动4个单位,求这一过程中F点移动的路程是多少?
相关试题

