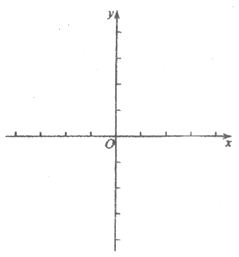
【题目】在平面直角坐标系xOy中,抛物线C:y=mx2+4x+1.
(1)当抛物线C经过点A(-5,6)时,求抛物线的表达式及顶点坐标;
(2)当直线y=-x+l与直线y=x+3关于抛物线C的对称轴对称时,求m的值;
(3)若抛物线C:y=mx2+4x+l(m>0)与x轴的交点的横坐标都在-l和0之间(不包括-l和0).结合函数的图象,求m的取值范围.
参考答案:
【答案】(1)y=x2+4x+1,抛物线的顶点坐标是(-2,-3);(2)m=2;(3)3<m≤4.
【解析】试题分析:(1)把点A(-5,6)代入抛物线y=mx2+4x+1求出m的值,即可得出抛物线的表达式与顶点坐标;
(2)先求出直线y=-x+1与直线y=x+3的交点,即可得出其对称轴,根据抛物线的对称轴方程求出m的值即可;
(3)根据抛物线C:y=mx2+4x+1(m>0)与x轴的交点的横坐标都在-1和0之间可知当x=-1时,y>0,且△≥0,求出m的取值范围即可.
试题解析:
(1)∵抛物线C:y=mx2+4x+1经过点A(-5,6),
∴6=25m-20+1,解得m=1,
∴抛物线的表达式为y=x2+4x+1=(x+2)2-3,
∴抛物线的顶点坐标为(-2,-3);
(2)∵直线y=-x+1与直线y=x+3的交点为(-1,2),
∴两直线的对称轴为直线x=-1.
∵直线y=-x+1与直线y=x+3关于抛物线C的对称轴对称,
∴-![]() =-1,解得m=2;
=-1,解得m=2;
(3)∵抛物线C:y=mx2+4x+1(m>0)与x轴的交点的横坐标都在-1和0之间,
∴当x=-1时,y>0,且△≥0,即
![]()
解得3<m≤4.
-
科目: 来源: 题型:
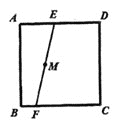
查看答案和解析>>【题目】如图,E,F分别是正方形ABCD边AD、BC上的两定点,M是线段EF上的一点,过M的直线与正方形ABCD的边交于点P和点H,且PH=EF,则满足条件的直线PH最多有( )条
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年中国快递行业竞争激烈,为了占据市场赢得消费者青睐,某快递公司出台了市内快件收费标准:凡是重庆市内的快递统一收取基础费用8元,快递质量不超过10kg,不加收费用;快递质量大于10kg,则超过10g的部分按0.3元/kg收费.
(1)某同学需要将重量为x(x>10)千克的书籍在重庆市内同城快递回家,则该同学需付快递费用y元,用含x的代数式表示y.
(2)因国庆阅兵需要将一些纪念品从重庆寄往相距1800千米的北京,该快递公司获得这项任务后,调整了市外快件收费标准,收费标准如下表.已知纪念品重量为a千克,则纪念品从重庆运往北京的快递费为多少元?(用含a的代数式表示w)
价格表
重量费
距离费
不超过10kg统一收取5元
0.01元/km
超过10kg不超过50kg的部分0.2元/kg
超过50kg部分0.4元/kg
(注:快递费=重量费+距离费)
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学的趣味无处不在,在学习数学的过程中,小明发现了有规律的等式:
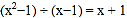 ;
; ;
;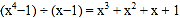 ;
;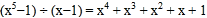 ;
;……
(1)从计算过程中找出规律,可知:
①
 ;
; ② =
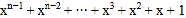 .
.(2)计算:
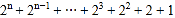 (结果用含n的式子表示)
(结果用含n的式子表示)(3)对于算式:
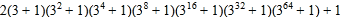
①计算出算式的值(结果用乘方表示);
②直接写出结果的个位数字是几?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若八个数据x1, x2, x3, ……x8, 的平均数为8,方差为1,增加一个数据8后所得的九个数据x1, x2, x3, …x8;8的平均数
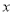 ________8,方差为S2 ________1.(填“>”、“=”、“<”)
________8,方差为S2 ________1.(填“>”、“=”、“<”) -
科目: 来源: 题型:
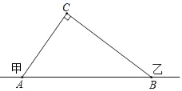
查看答案和解析>>【题目】在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问:在进行爆破时,公路AB段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,M,N,P,R分别是数轴上的四个整数所对应的点,其中有一个点是原点,并且,MN=NP=PR=1,数a对应的点在M和N之间,数b对应的点在P和R之间,若|a|+|b|=2,则原点是(填M,N,P,R中的一个或几个)_____________

相关试题

