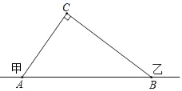
【题目】在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问:在进行爆破时,公路AB段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
参考答案:
【答案】AB段公路需要暂时封锁.
【解析】
如图,本题需要判断点C到AB的距离是否小于250米,如果小于则有危险,大于则没有危险.因此过C作CD⊥AB于D,然后根据勾股定理在直角三角形ABC中即可求出AB的长度,然后利用三角形的公式即可求出CD,然后和250米比较大小即可判断需要暂时封锁.
解:公路AB需要暂时封锁.
理由如下:如图,过C作CD⊥AB于D.
因为BC=400米,AC=300米,∠ACB=90°,
所以根据勾股定理有AB=500米.
因为S△ABC=![]() ABCD=
ABCD=![]() BCAC
BCAC
所以CD=![]() =240(米).
=240(米).
由于240米<250米,故有危险,
因此AB段公路需要暂时封锁.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有三个点
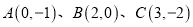 ,
,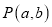 是
是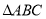 的边
的边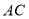 上一点,
上一点,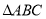 经平移后得到
经平移后得到 ,点
,点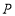 的对应点为
的对应点为 .
.(1)画出平移后的
 ,写出点
,写出点 的坐标;
的坐标;(2)
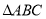 的面积为_________________;
的面积为_________________;(3)若点
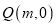 是
是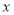 轴上一动点,
轴上一动点,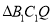 的面积为
的面积为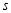 ,求
,求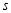 与
与 之间的关系式(用含
之间的关系式(用含 的式子表示
的式子表示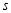 )
)
-
科目: 来源: 题型:
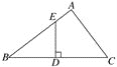
查看答案和解析>>【题目】已知,如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2-EA2=AC2,
(1)求证:∠A=90°.
(2)若DE=3,BD=4,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器商店计划从厂家购进
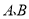 两种不同型号的电风扇,若购进8台
两种不同型号的电风扇,若购进8台 型和20台
型和20台 型电风扇,需资金7600元,若购进4台
型电风扇,需资金7600元,若购进4台 型和15台
型和15台 型电风扇,需资金5300元.
型电风扇,需资金5300元.(1)求
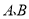 型电风扇每台的进价各是多少元;
型电风扇每台的进价各是多少元;(2)该商店经理计划进这两种电风扇共50台,而可用于购买这两种电风扇的资金不超过12800元,根据市场调研,销售一台
 型电风扇可获利80元,销售一台
型电风扇可获利80元,销售一台 型电风扇可获利120元.若两种电扇销售完时,所获得的利润不少于5000元.问有哪几种进货方案?哪种方案获得最大?最大利润是多少?
型电风扇可获利120元.若两种电扇销售完时,所获得的利润不少于5000元.问有哪几种进货方案?哪种方案获得最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
(1)求证:
 ;
;(2)求△AMN的面积(用a,b,c的代数式表示);
(3)当∠MAN=45°时,求证:c2=2ab.

-
科目: 来源: 题型:
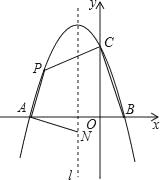
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,
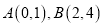 ,将线段
,将线段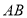 平移得到线段
平移得到线段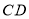 ,点
,点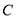 的坐标为
的坐标为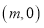 ,连结
,连结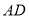 .
.(1)点
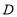 的坐标为__________________(用含
的坐标为__________________(用含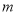 的式子表示);
的式子表示);(2)若
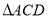 的面积为4,求点
的面积为4,求点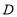 的坐标;
的坐标;(3)如图2,在(2)的条件下,延长
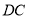 交
交 轴于点
轴于点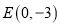 ,延长
,延长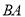 交
交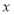 轴于
轴于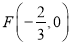 ,
, 是
是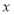 轴上一动点,
轴上一动点,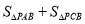 的值记为
的值记为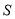 ,在点
,在点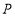 运动的过程中,
运动的过程中,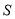 的值是否发生变化,若不变,请求出
的值是否发生变化,若不变,请求出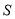 的值,并写出此时
的值,并写出此时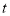 的取值范围,若变化,说明理由.
的取值范围,若变化,说明理由.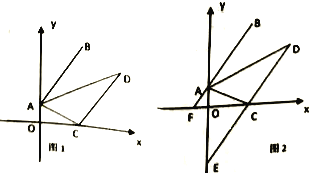
相关试题

