【题目】如图,E,F分别是正方形ABCD边AD、BC上的两定点,M是线段EF上的一点,过M的直线与正方形ABCD的边交于点P和点H,且PH=EF,则满足条件的直线PH最多有( )条
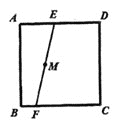
A.1B.2C.3D.4
参考答案:
【答案】C
【解析】
如图1,过点B作BG∥EF,过点C作CN∥PH,利用正方形的性质,可证得AB∥CD,AD∥BC,∠A=∠NBC=90°,AB=BC,再证明BG=CN,利用HL证明Rt△ABG≌Rt△CBN,根据全等三角形的对应角相等,可知∠ABG=∠BCN,然后证明PH⊥EF即可,因此过点M作EF的垂线满足的有一条直线;图2中还有2条,即可得出答案.
解:如图1,过点B作BG∥EF,过点C作CN∥PH,
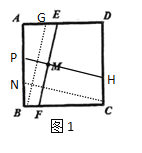
∵正方形ABCD,
∴AB∥CD,AD∥BC,∠A=∠NBC=90°,AB=BC,
∴四边形BGEF,四边形PNCH是平行四边形,
EF=BG,PH=CN,
∵PH=EF,
∴BG=CN,
在Rt△ABG和Rt△CBN中,
![]()
∴Rt△ABG≌Rt△CBN(HL)
∴∠ABG=∠BCN,
∵∠ABG+∠GBC=90°
∴∠BCN+∠GBC=90°,
∴BG⊥CN,
∴PH⊥EF,
∴过点M作EF的垂线满足的有一条直线;
如图2

图2中有两条P1H1,P2H2,
所以满足条件的直线PH最多有3条,
故答案为:C
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.
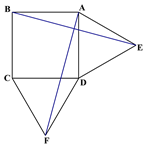
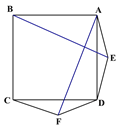

(图1) (图2) (备用图)
(1)请判断:AF与BE的数量关系是_____________,位置关系______________;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是一个正方体的表面展开图,请回答下列问题:
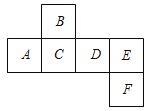
(1)与面B、面C相对的面分别是 和 ;
(2)若A=a3+
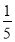 a2b+3,B=﹣
a2b+3,B=﹣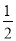 a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣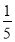 (a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
(a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式. -
科目: 来源: 题型:
查看答案和解析>>【题目】2019年中国快递行业竞争激烈,为了占据市场赢得消费者青睐,某快递公司出台了市内快件收费标准:凡是重庆市内的快递统一收取基础费用8元,快递质量不超过10kg,不加收费用;快递质量大于10kg,则超过10g的部分按0.3元/kg收费.
(1)某同学需要将重量为x(x>10)千克的书籍在重庆市内同城快递回家,则该同学需付快递费用y元,用含x的代数式表示y.
(2)因国庆阅兵需要将一些纪念品从重庆寄往相距1800千米的北京,该快递公司获得这项任务后,调整了市外快件收费标准,收费标准如下表.已知纪念品重量为a千克,则纪念品从重庆运往北京的快递费为多少元?(用含a的代数式表示w)
价格表
重量费
距离费
不超过10kg统一收取5元
0.01元/km
超过10kg不超过50kg的部分0.2元/kg
超过50kg部分0.4元/kg
(注:快递费=重量费+距离费)
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学的趣味无处不在,在学习数学的过程中,小明发现了有规律的等式:
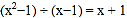 ;
; ;
;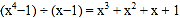 ;
;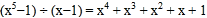 ;
;……
(1)从计算过程中找出规律,可知:
①
 ;
; ② =
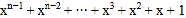 .
.(2)计算:
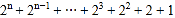 (结果用含n的式子表示)
(结果用含n的式子表示)(3)对于算式:
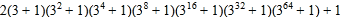
①计算出算式的值(结果用乘方表示);
②直接写出结果的个位数字是几?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线C:y=mx2+4x+1.
(1)当抛物线C经过点A(-5,6)时,求抛物线的表达式及顶点坐标;
(2)当直线y=-x+l与直线y=x+3关于抛物线C的对称轴对称时,求m的值;
(3)若抛物线C:y=mx2+4x+l(m>0)与x轴的交点的横坐标都在-l和0之间(不包括-l和0).结合函数的图象,求m的取值范围.
相关试题

