【题目】如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=8,DF=4,则菱形ABCD的边长为多少?
参考答案:
【答案】【解答】如图,连接OM,
根据菱形的对角线互相垂直平分,得OD=4,即圆的半径是8,
在直角△AOM中,OM=8,AM=4
根据勾股定理,得OA=![]() ,
,
在直角△AOD中,根据勾股定理得到:AD=![]() =8
=8
即菱形的边长是8.
【解析】根据菱形的性质和勾股定理求解.综合运用了菱形的性质以及勾股定理.
【考点精析】掌握勾股定理的概念和菱形的性质是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
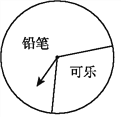
查看答案和解析>>【题目】某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(如图所示).下表是活动进行中的一组统计数据:
转动转盘
的次数n
100
150
200
500
800
1 000
落在“铅笔”
区域的次数m
68
111
136
345
564
701
落在“铅笔”
区域的频率
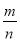
(1)计算并完成表格.
(2)请估计,当n很大时,落在“铅笔”区域的频率将会接近多少?
(3)假如你去转动该转盘一次,你获得哪种奖品的机会大?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少?
-
科目: 来源: 题型:
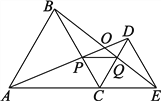
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中完全正确的是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组图形一定相似的是( )
A.两个直角三角形B.两个等边三角形C.两个菱形D.两个矩形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,一元二次方程x2﹣8x+15=0的两根分别是⊙O1和⊙O2的半径,当⊙O1和⊙O2相切时,O1O2的长度是( )
A.2
B.8
C.2或8
D.2<O1O2<8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示, AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=2AD,E是CD上一点,且AE=AB,则∠CBE的度数是多少?

相关试题

