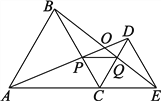
【题目】如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中完全正确的是___________.
参考答案:
【答案】①②③⑤
【解析】试题解析:①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,
∴AC=BC,EC=DC,∠BCE=∠ACD=![]()
∴△ACD≌△ECB
∴AD=BE,故本选项正确;
②∵△ACD≌△ECB
∴∠CBQ=∠CAP,
又∵∠PCQ=∠ACB=![]() CB=AC,
CB=AC,
∴△BCQ≌△ACP,
∴CQ=CP,又∠PCQ=![]()
∴△PCQ为等边三角形,
∴∠QPC=![]() =∠ACB,
=∠ACB,
∴PQ∥AE,故本选项正确;
③∵∠ACB=∠DCE=![]()
∴∠BCD=![]()
∴∠ACP=∠BCQ,
∵AC=BC,∠DAC=∠QBC,
∴△ACP≌△BCQ(ASA),
∴CP=CQ,AP=BQ,故本选项正确;
④已知△ABC、△DCE为正三角形,
故∠DCE=∠BCA=![]() ∠DCB=
∠DCB=![]()
又因为∠DPC=∠DAC+∠BCA,∠BCA=60∠DPC>![]()
故DP不等于DE,故本选项错误;
⑤∵△ABC、△DCE为正三角形,
∴∠ACB=∠DCE=![]() AC=BC,DC=EC,
AC=BC,DC=EC,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB,
∵∠ACB=∠CBE+∠CEB=![]()
∴∠AOB=![]()
故本选项正确.
综上所述,正确的结论是①②③⑤.
故答案为:①②③⑤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为参加学校的“我爱古诗词”知识竞赛,英英所在班级组织了古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计.以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
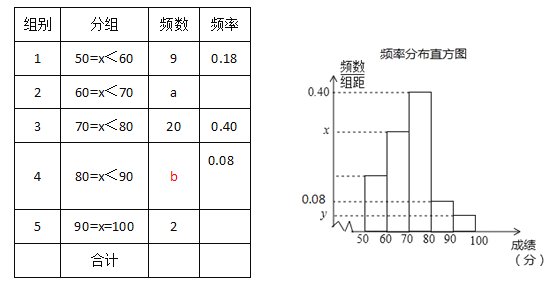
请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出a、b、x、y的值;
(2)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:五位同学请用A、B、C、D、E表示,其中小明为A,小敏为B)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.

-
科目: 来源: 题型:
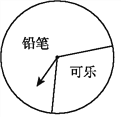
查看答案和解析>>【题目】某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(如图所示).下表是活动进行中的一组统计数据:
转动转盘
的次数n
100
150
200
500
800
1 000
落在“铅笔”
区域的次数m
68
111
136
345
564
701
落在“铅笔”
区域的频率
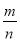
(1)计算并完成表格.
(2)请估计,当n很大时,落在“铅笔”区域的频率将会接近多少?
(3)假如你去转动该转盘一次,你获得哪种奖品的机会大?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组图形一定相似的是( )
A.两个直角三角形B.两个等边三角形C.两个菱形D.两个矩形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=8,DF=4,则菱形ABCD的边长为多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,一元二次方程x2﹣8x+15=0的两根分别是⊙O1和⊙O2的半径,当⊙O1和⊙O2相切时,O1O2的长度是( )
A.2
B.8
C.2或8
D.2<O1O2<8
相关试题

