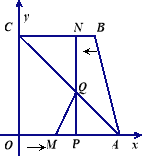
【题目】如图, 四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点![]() 从
从![]() 出发以每秒2个单位长度的速度向
出发以每秒2个单位长度的速度向![]() 运动;点
运动;点![]() 从
从![]() 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向![]() 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,连结AC交NP于Q,连结MQ.
,连结AC交NP于Q,连结MQ.
【1】点 (填M或N)能到达终点;
【1】求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
【1】是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,
![]() 说明理由.
说明理由.
参考答案:
【答案】
【1】点M
【1】经过t秒时,![]() ,
, ![]() ,则
,则![]() ,
,![]()
∵![]() =
=![]() =
=![]() ,∴
,∴![]() ∴
∴![]()
∴![]()
![]()
∴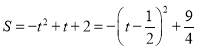 ∵
∵![]() ∴当
∴当![]() 时,S的值最大.
时,S的值最大.
【1】存在。
设经过t秒时,NB=t,OM=2t ,则![]() ,
,![]() ∴
∴![]() =
=![]() =
=![]()
①若![]() ,则
,则![]() 是等腰Rt△
是等腰Rt△![]() 底边
底边![]() 上的高,
上的高,
∴![]() 是底边
是底边![]() 的中线 ∴
的中线 ∴![]() ,∴
,∴![]() ,∴
,∴![]() , ∴点
, ∴点![]() 的坐标为(1,0)
的坐标为(1,0)
②若![]() ,此时
,此时![]() 与
与![]() 重合,∴
重合,∴![]() ,∴
,∴![]() ,
,
∴![]() ∴点
∴点![]() 的坐标为(2,0)
的坐标为(2,0)
【解析】
【1】由于点M比点N先出发并且点M的速度比点N大,可知点M能到达终点.
【1】经过t秒时可得NB=y,OM-2t.根据∠BCA=∠MAQ=45°推出QN=CN,PQ的值.求出S与t的函数关系式后根据t的值求出S的最大值.
【1】本题分两种情况讨论(若∠AQM=90°,PQ是等腰Rt△MQA底边MA上的高;
若∠QMA=90°,QM与QP重合)求出t值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对;
(2)如果∠AOD=50°,求∠DOP的度数.
(3)OP平分∠EOF吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式
 5+
5+ 3+
3+ =M ,当
=M ,当 =0时,M=-5,当
=0时,M=-5,当 =-3时,M=7,那么当
=-3时,M=7,那么当 =3时,M_______.
=3时,M_______. -
科目: 来源: 题型:
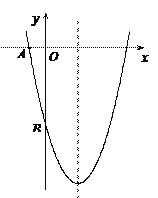
查看答案和解析>>【题目】如图,已知二次函数
 的图象与坐标轴交于点A(-1, 0)和点B(0,-5).
的图象与坐标轴交于点A(-1, 0)和点B(0,-5).(1)求该二次函数的解析式;
(2)已知该函数图象的对称轴上存在一点P,使得△ABP的周长最小.请求出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.

(1)证明:
 ;
;(2)若
 ,求当形ABCD的周长;
,求当形ABCD的周长;(3)在没有辅助线的前提下,图中共有_________对相似三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②
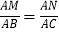 ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN=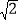 PC.其中正确的个数是( )
PC.其中正确的个数是( )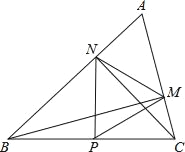
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数
 的图象经过
的图象经过 ,
, ,其中
,其中 ,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连结AD,DC,CB,AC与BD相交于点E.
,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连结AD,DC,CB,AC与BD相交于点E.
(1)若
 的面积为4,求点B的坐标;
的面积为4,求点B的坐标;(2)四边形ABCD能否成为平行四边形,若能,求点B的坐标,若不能说明理由;
(3)当
 时,求证:四边形ABCD是等腰梯形.
时,求证:四边形ABCD是等腰梯形.
相关试题

