【题目】如图,函数![]() 的图象经过
的图象经过![]() ,
,![]() ,其中
,其中![]() ,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连结AD,DC,CB,AC与BD相交于点E.
,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连结AD,DC,CB,AC与BD相交于点E.

(1)若![]() 的面积为4,求点B的坐标;
的面积为4,求点B的坐标;
(2)四边形ABCD能否成为平行四边形,若能,求点B的坐标,若不能说明理由;
(3)当![]() 时,求证:四边形ABCD是等腰梯形.
时,求证:四边形ABCD是等腰梯形.
参考答案:
【答案】(1)![]() ;(2)能,
;(2)能, ![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)将A的坐标代入反比例解析式中求出k的值,确定出反比例解析式,将B的坐标代入反比例解析式中,求出mn的值,三角形ABD的面积由BD为底边,AE为高,利用三角形面积公式来求,由B的坐标得到BD=m,由AC-EC表示出AE,由已知的面积,利用面积公式列出关系式,将mn的值代入,求出m的值,进而确定出n的值,即可得到B的坐标;
(2)假设四边形ABCD为平行四边形,利用平行四边形的性质得到BD与AC互相平分,得到E为AC的中点,E为BD的中点,由A的坐标求出E的坐标,进而确定出B的坐标,将B坐标代入反比例解析式检验,B在反比例图象上,故假设正确,四边形ABCD能为平行四边形;
(3)由由AC=BD,得到A的纵坐标与B的横坐标相等,确定出B的横坐标,将B横坐标代入反比例解析式中求出B的纵坐标,得到B的坐标,进而确定出E的坐标,得到DE=CE=1,由AC=BD,利用等式的性质得到AE=BE,进而得到两对对应边成比例,且由对顶角相等得到夹角相等,利用两边对应成比例且夹角相等的两三角形相似,得到三角形DEC与三角形AEB相似,由相似三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行得到CD与AB平行,而在直角三角形ADE与直角三角形BEC中,DE=EC,AE=BE,利用勾股定理得到AD=BC,且AD与BC不平行,可得出四边形ABCD为等腰梯形.
解:(1)![]() ;
;
(2)若ABCD是平行四边形,则AC,BD互相平分,
∵![]() ,∴
,∴![]() ,
,![]()
将![]() 代入反比例中,
代入反比例中,![]() ;
;
∴B在![]() 上,则四边形ABCD能成为平行四边形;
上,则四边形ABCD能成为平行四边形;
(3)∵![]() ,
,![]() ,
,![]() ;
;
∴![]()
∵![]() 轴,
轴,![]() 轴,
轴,
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
根据勾股定理,![]() .
.
∵AD与BC不平行
∴则四边形ABCD是等腰梯形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点
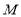 从
从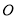 出发以每秒2个单位长度的速度向
出发以每秒2个单位长度的速度向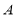 运动;点
运动;点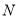 从
从 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点 作
作 垂直
垂直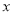 轴于点
轴于点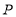 ,连结AC交NP于Q,连结MQ.
,连结AC交NP于Q,连结MQ. 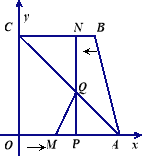
【1】点 (填M或N)能到达终点;
【1】求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
【1】是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,
 说明理由.
说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.

(1)证明:
 ;
;(2)若
 ,求当形ABCD的周长;
,求当形ABCD的周长;(3)在没有辅助线的前提下,图中共有_________对相似三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②
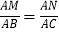 ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN=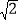 PC.其中正确的个数是( )
PC.其中正确的个数是( )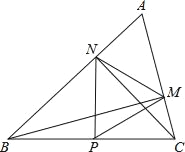
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】
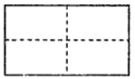
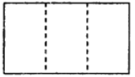
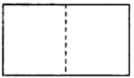
小明通过试验发现;将一个矩形可以分别成四个全等的矩形,三个全等的矩形,二个全等的矩形(如上图),于是他对含
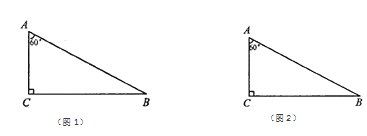
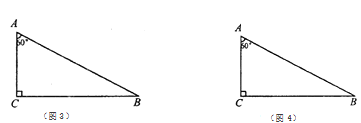
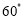 的直角三角形进行分别研究,发现可以分割成四个全等的三角形,三个全等的三角形.
的直角三角形进行分别研究,发现可以分割成四个全等的三角形,三个全等的三角形.(1)请你在图1,图2依次画出分割线,并简要说明画法;
(2)小明继续想分割成两个全等的三角形,发现比较困难.你能把这个直角三角形分割成两个全等的三角形吗?若能,画出分割线;若不能,请说明理由.(注:备用图不够用可以另外画)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一儿童服装商店在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”儿童节,商店决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装上盈利1200元,那么每件童装应降价多少元?
相关试题

