【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对;
(2)如果∠AOD=50°,求∠DOP的度数.
(3)OP平分∠EOF吗?为什么?

参考答案:
【答案】(1)①∠COP=∠BOP、②∠AOD=∠COB;(2)155°;(3)平分,理由见解析.
【解析】
(1)根据角平分线的性质和对顶角来填空;
(2)根据对顶角相等、角平分线的性质求得∠COP=![]() ∠AOD=25°;即可求出∠DOP的度数.
∠AOD=25°;即可求出∠DOP的度数.
(3)根据同角的余角相等得到∠EOC=∠BOF.根据角平分线的定义∠POC=∠POB,求得∠EOP=∠FOP.即可说明OP平分∠EOF.
(1)①∵OP是∠BOC的平分线,
∴∠COP=∠BOP.
②∵直线AB与CD相交于点O,
∴∠AOD=∠COB.
故答案是:∠COP=∠BOP、∠AOD=∠COB;
(2)∵∠AOD=∠BOC=50°,OP是∠BOC的平分线,
∴∠COP=![]() ∠AOD=25°.
∠AOD=25°.
∴∠DOP=180°-25°=155°;
(3)平分,理由如下:
∵如图,OE⊥AB,OF⊥CD,
∴∠EOB=90°,∠COF=90°,
∴∠EOB=∠COF,
∴∠EOC=∠BOF.
∵OP是∠BOC的平分线,
∴∠POC=∠POB,
∴∠EOP=∠FOP,
∴OP平分∠EOF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).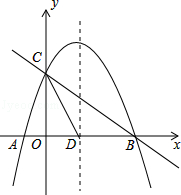
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=ax﹣a与y=
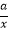 (a≠0)在同一直角坐标系中的图象可能是( )
(a≠0)在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
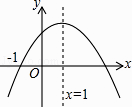
A.a>0
B.3是方程ax2+bx+c=0的一个根
C.a+b+c=0
D.当x<1时,y随x的增大而减小 -
科目: 来源: 题型:
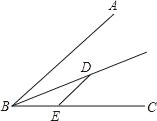
查看答案和解析>>【题目】如图,∠ABC=50°,BD平分∠ABC,过D作DE∥AB交BC于点E,若点F在AB上,且满足DF=DE,则∠DFB的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l的函数表达式是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=
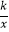 (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= 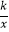 (k≠0)上的点D1处,则a= .
(k≠0)上的点D1处,则a= . 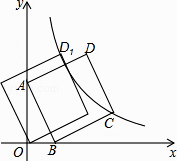
相关试题

