【题目】综合与实践
背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载于我国古代著名数学著作《周髀算经》中,为了方便,在本题中,我们把三边的比为3:4:5的三角形称为(3,4,5)型三角形,例如:三边长分别为9,12,15或3 ![]() ,4
,4 ![]() ,5
,5 ![]() 的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
实践操作 如图1,在矩形纸片ABCD中,AD=8cm,AB=12cm.
第一步:如图2,将图1中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图4,将图3中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.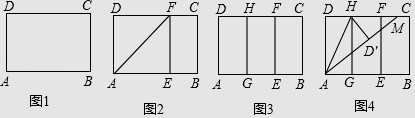
(1)请在图2中证明四边形AEFD是正方形.
(2)请在图4中判断NF与ND′的数量关系,并加以证明;
(3)请在图4中证明△AEN(3,4,5)型三角形;
(4)在不添加字母的情况下,图4中还有哪些三角形是(3,4,5)型三角形?请找出并直接写出它们的名称.
参考答案:
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴∠D=∠DAE=90°,
由折叠的性质得,AE=AD,∠AEF=∠D=90°,
∴∠D=∠DAE=∠AEF=90°,
∴四边形AEFD是矩形,
∵AE=AD,
∴矩形AEFD是正方形
(2)
解:NF=ND′,
理由:连接HN,
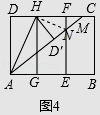
由折叠得,∠AD′H=∠D=90°,HF=HD=HD′,
∵四边形AEFD是正方形,
∴∠EFD=90°,
∵∠AD′H=90°,
∴∠HD′N=90°,
在Rt△HNF与Rt△HND′中, ![]() ,
,
∴Rt△HNF≌Rt△HND′,
∴NF=ND′
(3)
解:∵四边形AEFD是正方形,
∴AE=EF=AD=8cm,
由折叠得,AD′=AD=8cm,
设NF=xcm,则ND′=xcm,
在Rt△AEN中,
∵AN2=AE2+EN2,
∴(8+x)2=82+(8﹣x)2,
解得:x=2,
∴AN=8+x=10cm,EN=6cm,
∴EN:AE:AN=3:4:5,
∴△AEN是(3,4,5)型三角形
(4)
解:图4中还有△MFN,△MD′H,△MDA是(3,4,5)型三角形,
∵CF∥AE,
∴△CFN∽△AEN,
∵EN:AE:AN=3:4:5,
∴FN:CF:CN=3:4:5,
∴△MFN是(3,4,5)型三角形;
同理,△MD′H,△MDA是(3,4,5)型三角形.
【解析】(1)根据矩形的性质得到∠D=∠DAE=90°,由折叠的性质得得到AE=AD,∠AEF=∠D=90°,求得∠D=∠DAE=∠AEF=90°,得到四边形AEFD是矩形,由于AE=AD,于是得到结论;(2)连接HN,由折叠的性质得到∠AD′H=∠D=90°,HF=HD=HD′,根据正方形的想知道的∠HD′N=90°,根据全等三角形的性质即可得到结论;(3)根据正方形的性质得到AE=EF=AD=8cm,由折叠得,AD′=AD=8cm,设NF=xcm,则ND′=xcm,根据勾股定理列方程得到x=2,于是得到结论;(4)根据(3,4,5)型三角形的定义即可得到结论.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对相似三角形的应用的理解,了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
例如:方程
 的解为
的解为 ,不等式组
,不等式组 的解集为
的解集为 ,因为
,因为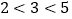 ,所以,称方程
,所以,称方程 为不等式组
为不等式组 的关联方程.
的关联方程.(1)在方程①
 ,②
,② ,③
,③ 中,不等式组
中,不等式组 的关联方程是 ;(填序号)
的关联方程是 ;(填序号)(2)若不等式组
 的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)(3)若方程
 ,
, 都是关于
都是关于 的不等式组
的不等式组 的关联方程,求
的关联方程,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.

(1)若AC=4,BC=2,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )

A. 400 B. 450 C. 500 D. 600
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
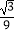 x2+
x2+ 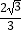 x+3
x+3 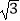 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).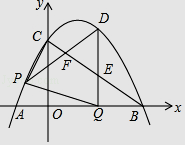
(1)求直线BC的函数表达式;
(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)
②在点P、Q运动的过程中,当PQ=PD时,求t的值;
(3)试探究在点P,Q运动的过程中,是否存在某一时刻,使得点F为PD的中点?若存在,请直接写出此时t的值与点F的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,I是△ABC三内角平分线的交点,IE⊥BC于E,AI延长线交BC于D,CI的延长线交AB于F,下列结论:①∠BIE=∠CID;②S△ABC=
 IE(AB+BC+AC);③BE=
IE(AB+BC+AC);③BE= (AB+BC﹣AC);④AC=AF+DC.其中正确的结论是_____.
(AB+BC﹣AC);④AC=AF+DC.其中正确的结论是_____.
-
科目: 来源: 题型:
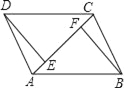
查看答案和解析>>【题目】已知,如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.
求证:(1)AF=CE;
(2)AB∥CD;
(3)AD=CB且AD∥CB.
相关试题

