【题目】如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )

A. 400 B. 450 C. 500 D. 600
参考答案:
【答案】A
【解析】延长BC交OD与点M,根据多边形的外角和为360°可得出∠OBC+∠MCD+∠CDM=140°,再根据四边形的内角和为360°即可得出结论.
解:延长BC交OD与点M,如图所示.

∵多边形的外角和为360°,
∴∠OBC+∠MCD+∠CDM=360°﹣220°=140°.
∵四边形的内角和为360°,
∴∠BOD+∠OBC+180°+∠MCD+∠CDM=360°,
∴∠BOD=40°.
故选A.
“点睛”本题考查了多边形的内角与外角以及角的计算,解题的关键是能够熟练的运用多边形的外角和为360°来解决问题.本题属于基础题,难度不大,解决该题型题目时,利用多边形的外角和与内角和定理,通过角的计算求出角的角度即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:﹣x3y+2x2y﹣xy= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△ABC的两条直角边的长a、b均为整数,且a为质数,若斜边c也是整数,求证:2(a+b+1)是完全平方数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断: ①OD⊥BC;②∠AOC=90°+
 ∠ABC;③OA=OB=OC;④OC平分∠ACB;⑤∠AOE+∠DCO=90°其中正确的有____
∠ABC;③OA=OB=OC;④OC平分∠ACB;⑤∠AOE+∠DCO=90°其中正确的有____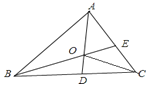
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m= .
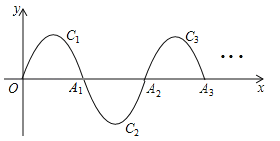
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x2-2x-m=0有两个相等的实数根,那么x2-mx-2=0的两根和是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l2于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l2于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为 .
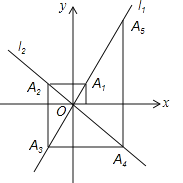
相关试题

