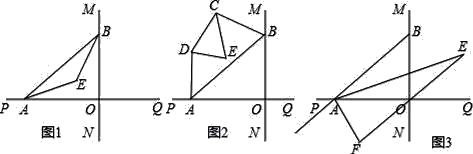
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
参考答案:
【答案】(1)135°;(2)67.5°;(3)60°, 45°
【解析】
(1)根据直线MN与直线PQ垂直相交于O可知∠AOB=90°,再由AE、BE分别是∠BAO和∠ABO的角平分线得出![]() ,
,![]() ,由三角形内角和定理即可得出结论;
,由三角形内角和定理即可得出结论;
(2)延长AD、BC交于点F,根据直线MN与直线PQ垂直相交于O可得出∠AOB=90°,进而得出![]() ,故
,故![]() ,再由AD、BC分别是∠BAP和∠ABM的角平分线,可知
,再由AD、BC分别是∠BAP和∠ABM的角平分线,可知![]() ,
,![]() ,由三角形内角和定理可知∠F=45°,再根据DE、CE分别是∠ADC和∠BCD的角平分线可知
,由三角形内角和定理可知∠F=45°,再根据DE、CE分别是∠ADC和∠BCD的角平分线可知![]() ,进而得出结论;
,进而得出结论;
(3))由∠BAO与∠BOQ的角平分线相交于E可知![]() ,
,![]() ,进而得出∠E的度数,由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°,在△AEF中,由一个角是另一个角的3倍分四种情况进行分类讨论.
,进而得出∠E的度数,由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°,在△AEF中,由一个角是另一个角的3倍分四种情况进行分类讨论.
(1)∠AEB的大小不变,
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴![]() ,
,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴![]() ,
,![]() ,
,
∴![]() °,
°,
∴∠AEB=135°;
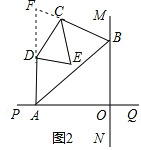
(2)∠CED的大小不变.
如图2,延长AD、BC交于点F.
∵直线MN与直线PQ垂直相交于O,
∴![]() °,
°,
∴![]() °,
°,
∴![]() °,
°,
∵AD、BC分别是∠BAP和∠ABM的角平分线,
∴![]() ,
,![]() ,
,
∴![]() °,
°,![]() °,
°,
∴![]() °,
°,
∴![]() °,
°,
∵DE、CE分别是∠ADC和∠BCD的角平分线,
∴![]() °,
°,
∴![]() °;
°;
(3)∵∠BAO与∠BOQ的角平分线相交于E,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴![]() °.
°.
在△AEF中,
∵有一个角是另一个角的3倍,故有:
①![]() ,
,![]() °,
°,![]() °;
°;
②![]() ,
,![]() °,
°,![]() °;
°;
③![]() ,
,![]() °,
°,![]() °;
°;
④![]() ,
,![]() °,
°,![]() °.
°.
∴∠ABO为60°或45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,求∠NOD.
(2)若∠1=
 ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD.
-
科目: 来源: 题型:
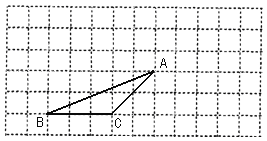
查看答案和解析>>【题目】(本题6分)如图,△ABC的顶点都在每个边长为1个单位长度的方格纸的格点上,将△ABC向右平移3格,再向上平移2格.
(1)请在图中画出平移后的
 ;
;(2)△ABC的面积为 _;
(3)若AB的长约为5.4,求出AB边上的高(结果保留整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )

A. 110° B. 120° C. 130° D. 140°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度数.
(2)若∠1=
 ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD. -
科目: 来源: 题型:
查看答案和解析>>【题目】布袋里有三个红球和两个白球,它们除了颜色外其他都相同,从布袋里摸出两个球,摸到两个红球的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P1(x1 , y1),点P2(x2 , y2),…,点Pn(xn , yn)在函数y=
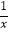 (x>0)的图象上,△P1OA,△P2A1A2 , △P3A2A3 , …,△PnAn﹣1An都是等腰直角三角形,斜边OA1 , A1A2 , A2A3 , …,An﹣1An都在x轴上(n是大于或等于2的正整数).若△P1OA1的内接正方形B1C1D1E1的周长记为l1 , △P2A1A2的内接正方形的周长记为l2 , …,△PnAn﹣1An的内接正方形BnCnDnEn的周长记为ln , 则l1+l2+l3+…+ln=(用含n的式子表示).
(x>0)的图象上,△P1OA,△P2A1A2 , △P3A2A3 , …,△PnAn﹣1An都是等腰直角三角形,斜边OA1 , A1A2 , A2A3 , …,An﹣1An都在x轴上(n是大于或等于2的正整数).若△P1OA1的内接正方形B1C1D1E1的周长记为l1 , △P2A1A2的内接正方形的周长记为l2 , …,△PnAn﹣1An的内接正方形BnCnDnEn的周长记为ln , 则l1+l2+l3+…+ln=(用含n的式子表示).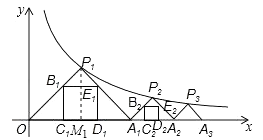
相关试题

