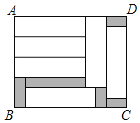
【题目】如图,在长方形ABCD中,放入6个形状和大小都相同的小长方形后,还有一部分空余(阴影部分),已知小长方形的长为a,宽为b,且a>b.
(1)用含a、b的代数式表示长方形ABCD的长AD和宽AB.
(2)用含a、b的代数式表示阴影部分的面积(列式表示即可,不要求化简).
(3)若a=7cm,b=2cm,求阴影部分的面积.
参考答案:
【答案】(1) AD=a+2b,AB=a+b;(2)a2﹣3ab+2b2;(3)15.
【解析】
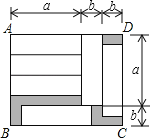
(1)如图所示,AD=a+b+b=a+2b,CD=a+b,即为长方形的长与宽;
(2)阴影部分的面积=长方形ABCD的面积-6个小长方形的面积,利用长方形的面积公式表示出阴影部分的面积即可;
(3)把a,b的值代入(2)中的代数式求解即可.
解:(1)由图形得:AD=a+2b,AB=a+b;
(2)S阴影=(a+b)(a+2b)﹣6ab
=a2+2ab+ab+2b2﹣6ab
=a2﹣3ab+2b2;
(3)把a=7cm,b=2cm代入,得
S阴影=72﹣3×7×2+2×22=15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,直线y=
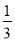 x与双曲线
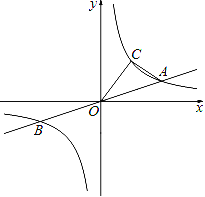
x与双曲线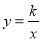 交于A、B两点,且点A的坐标为(6,m).
交于A、B两点,且点A的坐标为(6,m).(1)求双曲线
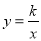 的解析式;
的解析式;(2)点C(n,4)在双曲线
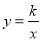 上,求△AOC的面积;
上,求△AOC的面积;(3)在(2)的条件下,在x轴上找出一点P,使△AOC的面积等于△AOP的面积的三倍.请直接写出所有符合条件的点P的坐标.
-
科目: 来源: 题型:
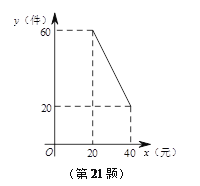
查看答案和解析>>【题目】某超市以20元/件的价格购进一批商品,根据前期销售情况,每天销售量y(件)与该商品的销售价x(元)之间的函数图象如图所示.
(1)求y与x之间的函数关系式.
(2)如果将该商品的销售价定为30元/件,不考虑其它因素,求该超市每天销售这种商品所能获得的利润.
(3)直接写出能使该超市获得最大利润的商品销售价
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.

(1)探究:线段OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,在平面直角坐标系中,A(﹣3,﹣4),B(0,﹣2).
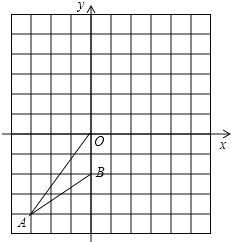
(1)△OAB绕O点旋转180°得到△OA1B1,请画出△OA1B1,并写出A1,B1的坐标;
(2)判断以A,B,A1,B1为顶点的四边形的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在一个长方形广场的四角都设计一块半径相同的四分之一圆形的花坛.若广场的长为m米,宽为n米,圆形的半径为r米.
(1)列式表示广场空地的面积.
(2)若广场的长为300米,宽为200米,圆形的半径为30米,求广场空地的面积(计算结果保留π).
(3)如图2所示,在(2)的条件下,若在广场的中间再建一个半径为R的圆形花坛,使广场的空地面积不少于广场总面积的
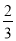 ,求R的最大整数值(π取3.1).
,求R的最大整数值(π取3.1).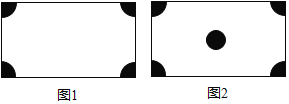
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,现有一张边长为4的正方形纸片
 ,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;

相关试题

