搜索
【题目】若|a+2|+（b﹣3）2=0，求（a+b）2016的值．
参考答案：
【答案】解：由题意得，a+2=0，b﹣3=0，
解得，a=﹣2，b=3，
则（a+b）2016=1
【解析】根据非负数的性质列出算式，求出a、b的值，计算即可．
【考点精析】关于本题考查的绝对值，需要了解正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0），其对称轴与x轴相交于点M．
（1）求抛物线的解析式和对称轴；
（2）在抛物线的对称轴上是否存在一点P，使△PAB的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）连接AC，在直线AC的下方的抛物线上，是否存在一点N，使△NAC的面积最大？若存在，请求出点N的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于二次三项式x2＋2ax＋a2这样的完全平方式，可以用公式法将它分解为(x＋a)2的形式，但是，对于一般二次三项式，就不能直接应用完全平方公式了，我们可以在二次三项式中先加上一项，使其成为完全平方式，再减去这项，使整个式子的值不变，如x2＋2ax－3a2＝x2＋2ax＋a2－a2－3a2＝(x＋a)2－(2a)2＝(x＋3a)(x－a)．像上面这样把二次三项式分解因式的方法叫做配方法．用上述方法把m2－6m＋8分解因式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知四边形OABC是边长为4的正方形，分别以OA，OC所在的直线为x轴、y轴，建立如图1所示的平面直角坐标系，直线l经过A，C两点．
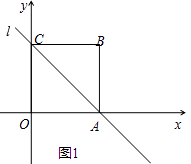
（1）写出点A，点C坐标并求直线l的函数表达式；
（2）若P是直线l上的一点，当△OPA的面积是5时，请求出点P的坐标；
（3）如图2，点D（3，﹣1），E是直线l上的一个动点，求出使|BE﹣DE|取得最大值时点E的坐标和最大值（不需要证明）．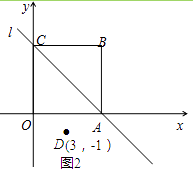
-
科目： 来源： 题型：
查看答案和解析>>【题目】一艘轮船位于灯塔P南偏西60°方向，距离灯塔20海里的A处，它向东航行多少海里到达灯塔P南偏西45°方向上的B处（参考数据：
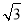≈1.732，结果精确到0.1）？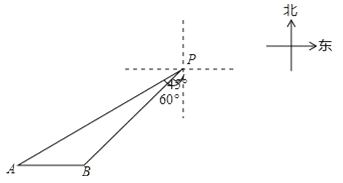
-
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，再求值：已知﹣2x3y4÷（﹣x2y2）（﹣x）﹣（x﹣2y）（2y＋x）＋x（x﹣xy2），其中x＝﹣1，y＝2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】利用因式分解简便计算57×99+44×99－99正确的是（）
A. 99×（57+44）=99×101=9999
B. 99×（57+44－1）=99×100=9900
C. 99×（57+44+1）=99×102=10096
D. 99×（57+44－99）=99×2=198
相关试题
