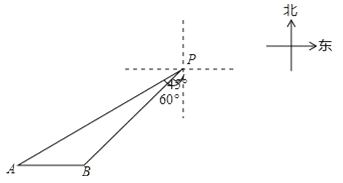
【题目】一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:![]() ≈1.732,结果精确到0.1)?
≈1.732,结果精确到0.1)?
参考答案:
【答案】7.3.
【解析】
试题分析:利用题意得到AC⊥PC,∠APC=60°,∠BPC=45°,AP=20,如图,在Rt△APC中,利用余弦的定义计算出PC=10,利用勾股定理计算出AC=![]() ,再判断△PBC为等腰直角三角形得到BC=PC=10,然后计算AC﹣BC即可.
,再判断△PBC为等腰直角三角形得到BC=PC=10,然后计算AC﹣BC即可.
试题解析:如图,AC⊥PC,∠APC=60°,∠BPC=45°,AP=20,在Rt△APC中,∵cos∠APC=![]() ,∴PC=20cos60°=10,∴AC=
,∴PC=20cos60°=10,∴AC=![]() =
=![]() ,在△PBC中,∵∠BPC=45°,∴△PBC为等腰直角三角形,∴BC=PC=10,∴AB=AC﹣BC=
,在△PBC中,∵∠BPC=45°,∴△PBC为等腰直角三角形,∴BC=PC=10,∴AB=AC﹣BC=![]() ﹣10≈7.3(海里).
﹣10≈7.3(海里).
答:它向东航行约7.3海里到达灯塔P南偏西45°方向上的B处.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次三项式x2+2ax+a2这样的完全平方式,可以用公式法将它分解为(x+a)2的形式,但是,对于一般二次三项式,就不能直接应用完全平方公式了,我们可以在二次三项式中先加上一项,使其成为完全平方式,再减去这项,使整个式子的值不变,如x2+2ax-3a2=x2+2ax+a2-a2-3a2=(x+a)2-(2a)2=(x+3a)(x-a).像上面这样把二次三项式分解因式的方法叫做配方法.用上述方法把m2-6m+8分解因式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形OABC是边长为4的正方形,分别以OA,OC所在的直线为x轴、y轴,建立如图1所示的平面直角坐标系,直线l经过A,C两点.
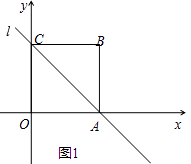
(1)写出点A,点C坐标并求直线l的函数表达式;
(2)若P是直线l上的一点,当△OPA的面积是5时,请求出点P的坐标;
(3)如图2,点D(3,﹣1),E是直线l上的一个动点,求出使|BE﹣DE|取得最大值时点E的坐标和最大值(不需要证明).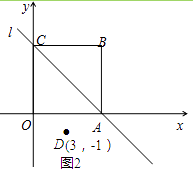
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a+2|+(b﹣3)2=0,求(a+b)2016的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:已知﹣2x3y4÷(﹣x2y2)(﹣x)﹣(x﹣2y)(2y+x)+x(x﹣xy2),其中x=﹣1,y=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用因式分解简便计算57×99+44×99-99正确的是()
A. 99×(57+44)=99×101=9999
B. 99×(57+44-1)=99×100=9900
C. 99×(57+44+1)=99×102=10096
D. 99×(57+44-99)=99×2=198
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人骑自行车从甲地到乙地,到达乙地他马上返回甲地.如图反映的是他离甲地的距离s(km)及他骑车的时间t(h)之间的关系,则下列说法正确的是( )
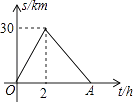
A.甲、乙两地之间的距离为60km
B.他从甲地到乙地的平均速度为30km/h
C.当他离甲地15km时,他骑车的时间为1h
D.若他从乙地返回甲地的平均速度为10km/h,则点A表示的数字为5
相关试题

