【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)抛物线的解析式为y=![]() x2﹣
x2﹣![]() x+4,对称轴是:直线x=3;(2)P点坐标为(3,
x+4,对称轴是:直线x=3;(2)P点坐标为(3, ![]() ),
),
理由见解析;(3)在直线AC的下方的抛物线上存在点N(![]() ,﹣3),使△NAC面积最大.
,﹣3),使△NAC面积最大.
【解析】(1)根据已知条件可设抛物线的解析式为y=a(x-1)(x-5).
把点A(0,4)代入上式,解得a=![]() .
.
∴y=![]() (x-1)(x-5)=
(x-1)(x-5)=![]() x2-
x2-![]() x+4=
x+4=![]() (x-3)2-
(x-3)2-![]() .
.
∴抛物线的对称轴是x=3.
(2)存在,P点的坐标是(3, ![]() ).如图1,连接AC交对称轴于点P,连接BP,AB.
).如图1,连接AC交对称轴于点P,连接BP,AB.
∵点B与点C关于对称轴对称,
∴PB=PC.
∴AB+AP+PB=AB+AP+PC=AB+AC.
∴此时△PAB的周长最小.
设直线AC的解析式为y=kx+b.把A(0,4),C(5,0)代入y=kx+b,得
![]() 解得
解得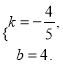
∴y=-![]() x+4.
x+4.
∵点P的横坐标为3,
∴y=-![]() ×3+4=
×3+4=![]() .
.
∴P(3, ![]() ).
).

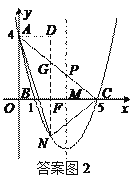
(3)在直线AC下方的抛物线上存在点N,使△NAC的面积最大.
如图2,设N点的横坐标为tt,此时点N(t, ![]() t2-
t2-![]() t+4)(0<t<5).
t+4)(0<t<5).
过点N作y轴的平行线,分别交x轴,AC于点F,G,过点A作AD⊥NG,垂足为D.
由(2)可知直线AC的解析式为y=-![]() x+4.
x+4.
把x=t代入y=-![]() x+4,得y=-
x+4,得y=-![]() t+4.
t+4.
∴G(t,- ![]() t+4).
t+4).
∴NG=-![]() t+4-(
t+4-(![]() t2-
t2-![]() t+4)=-
t+4)=-![]() t2+4t.
t2+4t.
∵AD+CF=OC=5,
∴S△NAC=S△ANG+S△CGN=![]() NG·AD+
NG·AD+![]() NG·CF=
NG·CF=![]() NG·OC
NG·OC
=![]() ×(-
×(-![]() t2+4t)×5=-2t2+10t=-2(t-
t2+4t)×5=-2t2+10t=-2(t-![]() )2+
)2+![]() .
.
∵当t=![]() 时,△NAC面积的最大值为
时,△NAC面积的最大值为![]() .
.
由t=![]() ,得y=
,得y=![]() ×(
×(![]() )2-
)2-![]() ×
×![]() +4=-3.
+4=-3.
∴N(![]() ,-3).
,-3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知深圳湾大酒店的三人间和双人间客房标价为:三人间为每人每天200元,双人间为每人每天300元.为吸引客源,促进旅游,在十一黄金周期间深圳湾大酒店进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间,双人间客房.
(1)如果每个客房正好住满,并且一天一共花去住宿费6300元.求租住了三人间、双人间客房各多少间?
(2)设三人间共住了x人,一天一共花去住宿费y元,请写出y与x的函数关系式;并请在直角坐标系内画出这个函数图象;
(3)一天6300元的住宿费是否为最低?如果不是,请设计一种入住的房间正好被住满的入住方案,使住宿费用最低,并求出最低的费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程ax2﹣bx+4=0的解是x=2,则2021+2a﹣b的值是( )
A. 2016B. 2018C. 2019D. 2022
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a与b互为相反数,c与d互为倒数,则a+b+3cd= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次三项式x2+2ax+a2这样的完全平方式,可以用公式法将它分解为(x+a)2的形式,但是,对于一般二次三项式,就不能直接应用完全平方公式了,我们可以在二次三项式中先加上一项,使其成为完全平方式,再减去这项,使整个式子的值不变,如x2+2ax-3a2=x2+2ax+a2-a2-3a2=(x+a)2-(2a)2=(x+3a)(x-a).像上面这样把二次三项式分解因式的方法叫做配方法.用上述方法把m2-6m+8分解因式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形OABC是边长为4的正方形,分别以OA,OC所在的直线为x轴、y轴,建立如图1所示的平面直角坐标系,直线l经过A,C两点.
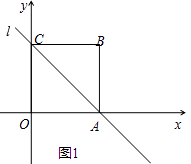
(1)写出点A,点C坐标并求直线l的函数表达式;
(2)若P是直线l上的一点,当△OPA的面积是5时,请求出点P的坐标;
(3)如图2,点D(3,﹣1),E是直线l上的一个动点,求出使|BE﹣DE|取得最大值时点E的坐标和最大值(不需要证明).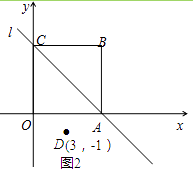
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a+2|+(b﹣3)2=0,求(a+b)2016的值.
相关试题

