【题目】我们都知道无限不循环小数是无理数,而无限循环小数是可以化成分数的。例如![]() (3为循环节)是可以化成分数的,方法如下:
(3为循环节)是可以化成分数的,方法如下:
令![]() ①
①
则![]() ②
②
②-①得![]()
![]()
![]()
所以![]() 可以化成分数为
可以化成分数为![]()
请你阅读上面材料完成下列问题:
(1)![]() (
(![]() )化成分数是 .
)化成分数是 .
(2)请你将![]() (
(![]() )化为分数.
)化为分数.
(3)请你将![]() (
(![]() )化为分数.
)化为分数.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)设0.777…=m,方程两边都乘以10,转化为7+m=10m,求出其解即可.
(2)令c=0.262626,则方程两边都乘以100,转化为100c-c=26,求出其解即可.
(3)d=0.1111…①,则10d=1.111…②,②-①得:10d-d=1,所以0.12111…=0.1111+0.01.
(1)令b=0.777…①
则10b=7.777…②
②①得10bb=7,
即9b=7,解得:b=![]() ,
,
故![]() 化成分数是
化成分数是![]() ;
;
(2)令c=0.262626…①
则100c=26.262626…②
②①得100cc=26,
即99c=26,解得:c=![]() ,
,
故将![]() 化成分数为
化成分数为![]() ;
;
(3)∵0.12111…=0.1111+0.01,
∴设d=0.1111…①,
则10d=1.111…②,
②①得:10dd=1,
即9d=1,
解得:d=![]() ,
,
则0.12111…=0.1111+0.01=![]() +
+![]() =
=![]()
故答案是:(1) ![]() (2)
(2)![]() ;(3)
;(3)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知已知抛物线
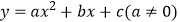 与x轴交于点
与x轴交于点 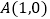 和点
和点 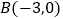 ,与y轴交于点C,且
,与y轴交于点C,且 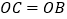 .
.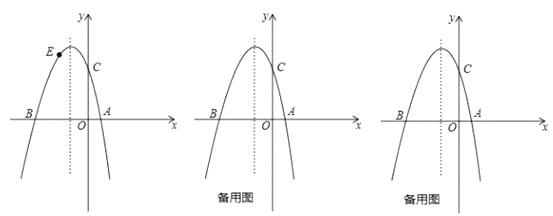
(1)求此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
(4)连AC,H是抛物线上一动点,过点H作AC的平行线交x轴于点F,是否这样的点F,使得以A,C,H,F为顶点的四边形是平行四边形?若存在,直接写出满足条件的点F的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司销售部为了定制下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的平均数、中位数、众数分别是( )

A.19,20,14
B.19,20,20
C.18.4,20,20
D.18.4,25,20 -
科目: 来源: 题型:
查看答案和解析>>【题目】数轴是一个非常重要的数学工具,它使数和数轴上的点建立对应关系,解释了数与点之间的内在联系,它是“数形结合”的基础。
如图,数轴上有三个点A、B、C,它们可以沿着数轴左右移动,请回答
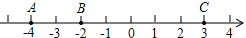 )
)(1)将点B向右移动4个单位长度后到达点D,点D表示的数是 ,A、D两点之间的距离是 ;
(2)移动点A到达E点,使B、C、E三点的其中某一点到其它两点的距离相等,写出点E在数轴上对应的数值 ;
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 0是绝对值最小的有理数 B. 如果
 的相反数是
的相反数是 5,那么
5,那么 5
5C. 若∣
 ∣
∣ ∣
∣ 4∣,那么
4∣,那么

 4 D. 任何非零有理数的平方都大于0
4 D. 任何非零有理数的平方都大于0 -
科目: 来源: 题型:
查看答案和解析>>【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线
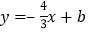 分别与
分别与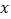 轴、
轴、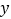 轴交于A、B两点,与直线
轴交于A、B两点,与直线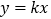 交于点C(2,
交于点C(2, ).平行于
).平行于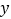 轴的直线l从原点O出发,以每秒1个单位长度的速度沿
轴的直线l从原点O出发,以每秒1个单位长度的速度沿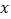 轴向右平移,到C点时停止;直线l分别交线段BC、OC、
轴向右平移,到C点时停止;直线l分别交线段BC、OC、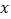 轴于点D、E、P,以DE为斜边向左侧作等腰直角△DEF,设直线l的运动时间为
轴于点D、E、P,以DE为斜边向左侧作等腰直角△DEF,设直线l的运动时间为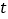 (秒).
(秒).(1)求
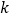 、
、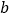 的值;
的值; (2)当
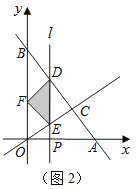
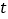 为何值时,点F在
为何值时,点F在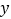 轴上(如图2);
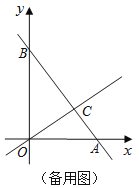
轴上(如图2);(3)设△DEF与△BCO重叠部分的面积为S,请求出S与
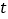 的函数关系式,并写出
的函数关系式,并写出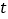 的取值范围.
的取值范围.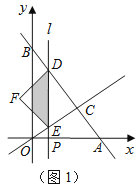
相关试题

