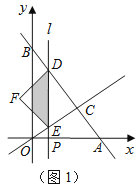
【题目】如图1,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于A、B两点,与直线
轴交于A、B两点,与直线![]() 交于点C(2,
交于点C(2,![]() ).平行于
).平行于![]() 轴的直线l从原点O出发,以每秒1个单位长度的速度沿
轴的直线l从原点O出发,以每秒1个单位长度的速度沿![]() 轴向右平移,到C点时停止;直线l分别交线段BC、OC、
轴向右平移,到C点时停止;直线l分别交线段BC、OC、![]() 轴于点D、E、P,以DE为斜边向左侧作等腰直角△DEF,设直线l的运动时间为
轴于点D、E、P,以DE为斜边向左侧作等腰直角△DEF,设直线l的运动时间为![]() (秒).
(秒).
(1)求![]() 、
、![]() 的值;
的值;
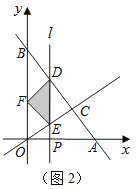
(2)当![]() 为何值时,点F在
为何值时,点F在![]() 轴上(如图2);
轴上(如图2);
(3)设△DEF与△BCO重叠部分的面积为S,请求出S与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)当
;(2)当![]() =1时,点F在
=1时,点F在![]() 轴上;(3)当0<t≤1时,S=﹣3t2+4t;当1<t<2时,S=(t﹣2)2.
轴上;(3)当0<t≤1时,S=﹣3t2+4t;当1<t<2时,S=(t﹣2)2.
【解析】分析:(1)利用待定系数法即可求得k和b的值;
(2)当F在y轴上时,F到DE的距离等于DE的长的一半,据此即可列方程求得t的值;
(3)分F在y轴的左侧和右侧两种情况进行讨论,当F在y轴的左侧时,阴影部分是两个等腰直角三角形面积的差,当F在y轴的右侧时,阴影部分就是△DEF的面积,根据三角形的面积公式即可求得函数的解析式.
详解:(1)把(2,![]() )代入y=﹣
)代入y=﹣![]() x+b得:﹣
x+b得:﹣![]() +b=
+b=![]() ,解得:b=4;
,解得:b=4;
把(2,![]() )代入y=kx中,2k=
)代入y=kx中,2k=![]() ,解得:k=
,解得:k=![]() .
.
故答案为:![]() ,4;
,4;
(2)由(1)得两直线的解析式为:
y=﹣![]() x+4和y=
x+4和y=![]() x,依题意得:OP=t,则D(t,﹣
x,依题意得:OP=t,则D(t,﹣![]() t+4),E(t,
t+4),E(t,![]() t),
t),
∴DE=﹣2t+4,作FG⊥DE于G,则FG=OP=t.
∵△DEF是等腰直角三角形,FG⊥DE,∴FG=![]() DE,即t=
DE,即t=![]() (﹣2t+4/span>),解得:t=1.
(﹣2t+4/span>),解得:t=1.
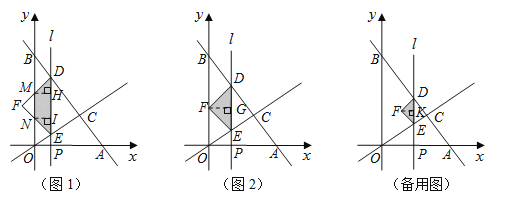
(3)当0<t≤1时(如图1),S△DEF=![]() (﹣
(﹣![]() t+4﹣
t+4﹣![]() t)
t)![]() (﹣
(﹣![]() t+4﹣
t+4﹣![]() t)=
t)=![]() (﹣2t+4)2=(t﹣2)2,在y轴的左边部分是等腰直角三角形,底边上的高是:
(﹣2t+4)2=(t﹣2)2,在y轴的左边部分是等腰直角三角形,底边上的高是:![]() (﹣
(﹣![]() t+4﹣
t+4﹣![]() t)﹣t=
t)﹣t=![]() (﹣2t+4)﹣t=2﹣2t,则面积是:(2﹣2t)2.
(﹣2t+4)﹣t=2﹣2t,则面积是:(2﹣2t)2.
S=(t﹣2)2﹣(2﹣2t)2=﹣3t2+4t;
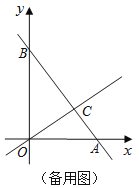
当1<t<2时(备用图),作FK⊥DE于点K.则:
S=(t﹣2)2.
综上所述:当0<t≤1时,S=﹣3t2+4t;当1<t<2时,S=(t﹣2)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们都知道无限不循环小数是无理数,而无限循环小数是可以化成分数的。例如
 (3为循环节)是可以化成分数的,方法如下:
(3为循环节)是可以化成分数的,方法如下:令
 ①
①则
 ②
②②-①得



所以
 可以化成分数为
可以化成分数为
请你阅读上面材料完成下列问题:
(1)
 (
( )化成分数是 .
)化成分数是 .(2)请你将
 (
( )化为分数.
)化为分数.(3)请你将
 (
( )化为分数.
)化为分数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 0是绝对值最小的有理数 B. 如果
 的相反数是
的相反数是 5,那么
5,那么 5
5C. 若∣
 ∣
∣ ∣
∣ 4∣,那么
4∣,那么

 4 D. 任何非零有理数的平方都大于0
4 D. 任何非零有理数的平方都大于0 -
科目: 来源: 题型:
查看答案和解析>>【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )
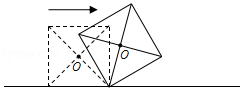
A.4a
B.2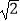 πa
πa
C.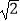
πa
D.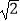
a -
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句错误的有( )
①近似数0.010精确到千分位
②如果两个角互补,那么一个是锐角,一个是钝角
③若线段
 ,则P一定是AB中点
,则P一定是AB中点④A与B两点间的距离是指连接A、B两点间的线段
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
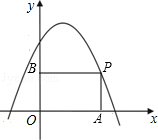
查看答案和解析>>【题目】如图,P是抛物线y=﹣x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为 .
相关试题

