【题目】2016年中考前,张老师为了解全市初三男生体育考试项目的选择情况(每人限选一项),在全市范围内随机调查了部分初三男生,将调查结果分成五类:A.推实心球(2kg);B.立定跳远;C.半场运球;D.跳绳;E.其他.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)将上面的条形统计图补充完整;
(2)假定全市初三毕业学生中有32000名男生,试估计全市初三男生中选半场运球的人数有多少人?
(3)甲、乙两名初三男生在上述选择率较高的三个项目:B.立定跳远;C.半场运球;D.跳绳中各选一项,同时选半场运球、立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果.
参考答案:
【答案】
(1)
解:被调查的学生总人数:150÷15%=1000(人),
选择B的人数:1000×(1-15%-20%-40%-5%)=1000×20%=200(人);
补全统计图如图所示.

(2)
解:32000×40%=12800(人).
(3)
解:根据题意画出如下树形图:

所有等可能结果有9种:BB、BC、BD、CB、CC、CD、DB、DC、DD,
同时选择B和D的有2种可能,即BD和DB,
P(同时选择B和D)= ![]() .
.
【解析】(1)根据选A的有150人,占调查人数的15%,则可求出调查总人数,先求出B所占的百分比,再由调查总人数×选B的百分比,求出选B的人数;(2)选半场运球的占40%,乘以总人数,即可求得;(3)列出所有等可能的结果数,再找出“同时选择B和D”的情况数量,则可求得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图,其对称轴为直线x=1,给出下列结论:
①b2-4ac>0;②2a+b=0;③abc>0;④3a+c>0.
则正确的结论个数为( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的顶点A、C在双曲线y1=
 上,B、D在双曲线y2=
上,B、D在双曲线y2=  上,k1=2k2(k1>0),AB//y轴,S□ABCD=24,则k1=.
上,k1=2k2(k1>0),AB//y轴,S□ABCD=24,则k1=.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
(1)当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.给出以下结论:①DG=DF;②四边形EFDG是菱形;③EG2=
 GF×AF;④当AG=6,EG=2
GF×AF;④当AG=6,EG=2 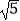 时,BE的长为
时,BE的长为 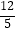
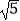 ,其中正确的结论个数是( )
,其中正确的结论个数是( ) 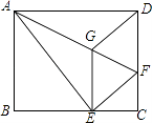
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60度,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45度,已知山坡AB的坡度i=1:
 ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.(保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】某工程,乙工程队单独先做10天后,再由甲,乙两个工程队合作20天就能完成全部工程,已知甲工程队单独完成此工程所需天数是乙工程队单独完成此工程所需天数的
 ,
,
(1)求:甲,乙工程队单独做完成此工程各需多少天?
(2)甲工程队每天的费用为0.67万元,乙工程队每天的费用为0.33万元,该工程的预算费用为20万元,若甲,乙工程队一起合作完成该工程,请问工程费用是否够用,若不够用应追加多少万元?
相关试题

