【题目】如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-![]() x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
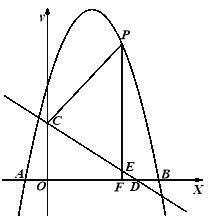
(1)求抛物线的解析式;(2)若PE=5EF,求m的值;(3)若点E′是点E关于直线PC的对称点、是否存在点P,使点E/落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由。
参考答案:
【答案】(1)、y=-![]() +4x+5;(2)、m=2或m=
+4x+5;(2)、m=2或m=![]() ;(3)、
;(3)、![]() ,
,![]() (4,5),
(4,5),![]() .
.
【解析】
试题分析:(1)、利用待定系数法进行求解;(2)、首先设出点P、点E和点F的坐标,求出PE的长度,然后根据点E在点F的上方和下方两种情况分别进行计算;(3)、根据△CME和△COD相似来进行求解.
试题解析:(1)、将A、B两点的坐标代入得:![]() 解得:
解得:![]()
∴抛物线的解析式为:y=-![]() +4x+5
+4x+5
、设点P的坐标为(m,-![]() +4m+5),则E(m,-
+4m+5),则E(m,-![]() m+3),F(m,0)
m+3),F(m,0)
∵点P在x轴上方,要使PE=5EF,点P应在y轴右侧 ∴0<m<5
PE=-![]() +4m+5-(-
+4m+5-(-![]() m+3)=-
m+3)=-![]() +
+![]() m+2
m+2
①当点E在点F上方时,EF=-![]() m+3 ∵PE=5EF ∴-
m+3 ∵PE=5EF ∴-![]() +
+![]() m+2=5(-
m+2=5(-![]() m+3)
m+3)
解得:![]() =2,
=2,![]() (舍去)
(舍去)
②当点E在点F下方时,EF=![]() m-3 ∵PE=5EF ∴-
m-3 ∵PE=5EF ∴-![]() +
+![]() m+2=5(
m+2=5(![]() m-3)
m-3)
解得:![]() ,
,(舍去)
(3)、点P的坐标为![]() ,
,![]() (4,5),
(4,5),![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,AB、AC是圆O的两条弦,AB=AC,过圆心O作OH⊥AC于点H.

(1)如图1,求证:∠B=∠C;
(2)如图2,当H、O、B三点在一条直线上时,求∠BAC的度数;
(3)如图3,在(2)的条件下,点E为劣弧BC上一点,CE=6,CH=7,连接BC、OE交于点D,求BE的长和
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)同题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC的度数.
小明想到一种方法,但是没有解答完:
如图2,过P作PE∥AB,∴∠APE+∠PAB=180°.
∴∠APE=180°-∠PAB=180°-130°=50°.
∵AB∥CD.∴PE∥CD.
…………
请你帮助小明完成剩余的解答.
(2)问题迁移:请你依据小明的思路,解答下面的问题:
如图3,AD∥BC,点P在射线OM上运动,∠MDP=∠α,∠BCP=∠β.
①当点P在A、B两点之间时,∠CPD,∠α,∠β之间有何数量关系?请说明理由.
②当点P在A、B两点外侧时(点P与点O不重合),请直接写出∠CPD,∠α,∠β之间的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
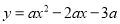 交X轴于点A、B(A左B右),交Y轴于点C,
交X轴于点A、B(A左B右),交Y轴于点C, 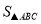
=6,点P为第一象限内抛物线上的一点.
(1)求抛物线的解析式;
(2)若∠PCB=45°,求点P的坐标;
(3)点Q为第四象限内抛物线上一点,点Q的横坐标比点P的横坐标大1,连接PC、
AQ,当PC=
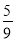 AQ时,求点P的坐标以及ΔPCQ的面积.
AQ时,求点P的坐标以及ΔPCQ的面积.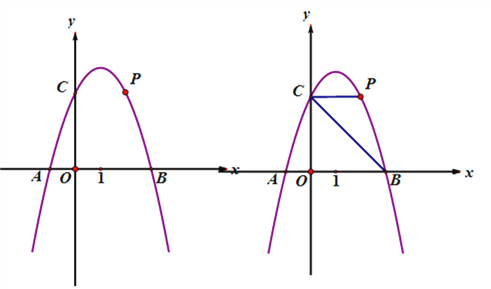
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.
(1)求证:△AOE≌△COF;
(2)若∠EOD=30°,求CE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 为锐角,点
为锐角,点 为直线
为直线 上一动点,以
上一动点,以 为直角边且在
为直角边且在 的右侧作等腰直角三角形
的右侧作等腰直角三角形 ,
, ,
, .
.
(1)如果
 ,
, .
.①当点
 在线段
在线段 上时,如图1,线段
上时,如图1,线段 、
、 的位置关系为___________,数量关系为_____________
的位置关系为___________,数量关系为_____________②当点
 在线段
在线段 的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.(2)如图3,如果
 ,
, ,点
,点 在线段
在线段 上运动。探究:当
上运动。探究:当 多少度时,
多少度时, ?小明通过(1)的探究,猜想
?小明通过(1)的探究,猜想 时,
时, .他想过点
.他想过点 做
做 的垂线,与
的垂线,与 的延长线相交,构建图2的基本图案,寻找解决此问题的方法。小明的想法对吗?如不对写出你的结论;如对按此方法解决问题并写出理由.
的延长线相交,构建图2的基本图案,寻找解决此问题的方法。小明的想法对吗?如不对写出你的结论;如对按此方法解决问题并写出理由. -
科目: 来源: 题型:
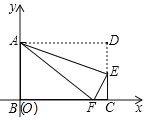
查看答案和解析>>【题目】如图,以矩形ABCD的相邻边建立直角坐标系,AB=3,BC=5.点E是边CD上一点,将△ADE沿着AE翻折,点D恰好落在BC边上,记为F.
(1)求折痕AE所在直线的函数解析式______;
(2)若把翻折后的矩形沿y轴正半轴向上平移m个单位,连结OF,若△OAF是等腰三角形,则m的值是______,
相关试题

