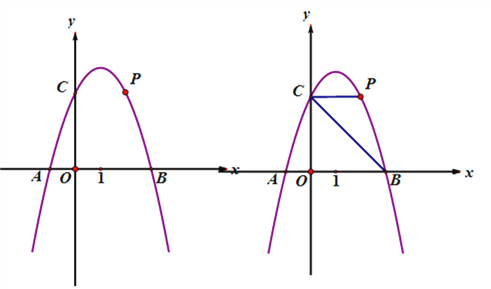
【题目】如图,抛物线![]() 交X轴于点A、B(A左B右),交Y轴于点C,
交X轴于点A、B(A左B右),交Y轴于点C, ![]()
=6,点P为第一象限内抛物线上的一点.
(1)求抛物线的解析式;
(2)若∠PCB=45°,求点P的坐标;
(3)点Q为第四象限内抛物线上一点,点Q的横坐标比点P的横坐标大1,连接PC、
AQ,当PC=![]() AQ时,求点P的坐标以及ΔPCQ的面积.
AQ时,求点P的坐标以及ΔPCQ的面积.
参考答案:
【答案】(1)y=x+2x+3;(2)P(2,3);(3)P(![]() ,
,![]() ),
), ![]() .
.
【解析】试题分析:(1)根据抛物线的解析式求得点A、B、C的坐标,根据, ![]() =6即可求得a值,从而求得抛物线的解析式;(2)根据点B、C的坐标判定△OBC是等腰直角三角形,即可得∠BCO=∠OBC=45°,已知点P为第一象限内抛物线上的一点,且∠PCB=45°,可得PC∥OB,所以P点的纵坐标为3,令y=3,解方程即可求得点P的横坐标,从而求得点P的坐标;(3)根据点P在第一象限,点Q在第二象限,且横坐标相差1,进而设出点P(3-m,-m2+4m)(0<m<1);得出点Q(4-m,-m2+6m-5),得出CP2,AQ2,最后建立方程求出m的值,从而求出点P、Q的坐标,再求出直线CQ的解析式及点D的坐标,根据S△PCQ=S△PCD+S△PQD即可求得ΔPCQ的面积.
=6即可求得a值,从而求得抛物线的解析式;(2)根据点B、C的坐标判定△OBC是等腰直角三角形,即可得∠BCO=∠OBC=45°,已知点P为第一象限内抛物线上的一点,且∠PCB=45°,可得PC∥OB,所以P点的纵坐标为3,令y=3,解方程即可求得点P的横坐标,从而求得点P的坐标;(3)根据点P在第一象限,点Q在第二象限,且横坐标相差1,进而设出点P(3-m,-m2+4m)(0<m<1);得出点Q(4-m,-m2+6m-5),得出CP2,AQ2,最后建立方程求出m的值,从而求出点P、Q的坐标,再求出直线CQ的解析式及点D的坐标,根据S△PCQ=S△PCD+S△PQD即可求得ΔPCQ的面积.
试题解析:
(1)∵抛物线y=ax2ax3a=a(x+1)(x3),
∴A(1,0),B(3,0),C(0,3a),
∴AB=4,OC=|3a|=|3a|,
∵S△ABC=6,
∴![]() ABOC=6,
ABOC=6,
∴![]() ×4×|3a|=6,
×4×|3a|=6,
∴a=1或a=1(舍),
∴抛物线的解析式为y=x+2x+3;
(2)由(1)知,B(3,0),C(0,3a),
∴C(0,3),
∴OB=3,OC=3,
∴△OBC是等腰直角三角形,
∴∠BCO=∠OBC=45°,
∵点P为第一象限内抛物线上的一点,且∠PCB=45°,
∴PC∥OB,
∴P点的纵坐标为3,
由(1)知,抛物线的解析式为y=x+2x+3,
令y=3,∴x+2x+3=3,
∴x=0(舍)或x=2,
∴P(2,3);
(3)如图2,过点P作PD⊥x轴交CQ于D,
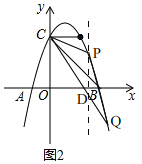
设P(3m,m+4m)(0<m<1);
∵C(0,3),
∴PC2=(3m) +(m+4m3)2=(m3) [(m1)+1],
∵点Q的横坐标比点P的横坐标大1,
∴Q(4m,m+6m5),
∵A(1,0).
∴AQ2=(4m+1)+(m+6m5)=(m5) [(m1)+1]
∵PC=![]() AQ,
AQ,
∴81PC=25AQ,
∴81(m3) [(m1) +1]=25(m5) [(m1)+1],
∵0<m<1,
∴[(m1)+1]≠0,
∴81(m3)=25(m5),
∴9(m3)=±5(m5),
∴m=![]() 或m=
或m=![]() (舍),
(舍),
∴P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),
),
∵C(0,3),
∴直线CQ的解析式为y=![]() x+3,
x+3,
∵P(![]() ,
,![]() ),
),
∴D(![]() ,
,![]() ),
),
∴PD=![]() +
+![]() =52,
=52,
∴S△PCQ=S△PCD+S△PQD=![]() PD×xP+
PD×xP+![]() PD×(xQxP)=
PD×(xQxP)= ![]() PD×xQ=
PD×xQ=![]() ×
×![]() ×
×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50分才乘上缆车,缆车的平均速度为180米/分,设小亮出发x分后行走的路程为y米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是_________米,他途中休息了___________分;
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度;
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,AB、AC是圆O的两条弦,AB=AC,过圆心O作OH⊥AC于点H.

(1)如图1,求证:∠B=∠C;
(2)如图2,当H、O、B三点在一条直线上时,求∠BAC的度数;
(3)如图3,在(2)的条件下,点E为劣弧BC上一点,CE=6,CH=7,连接BC、OE交于点D,求BE的长和
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)同题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC的度数.
小明想到一种方法,但是没有解答完:
如图2,过P作PE∥AB,∴∠APE+∠PAB=180°.
∴∠APE=180°-∠PAB=180°-130°=50°.
∵AB∥CD.∴PE∥CD.
…………
请你帮助小明完成剩余的解答.
(2)问题迁移:请你依据小明的思路,解答下面的问题:
如图3,AD∥BC,点P在射线OM上运动,∠MDP=∠α,∠BCP=∠β.
①当点P在A、B两点之间时,∠CPD,∠α,∠β之间有何数量关系?请说明理由.
②当点P在A、B两点外侧时(点P与点O不重合),请直接写出∠CPD,∠α,∠β之间的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-
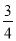 x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。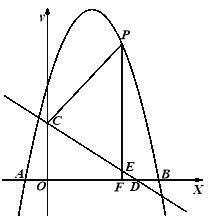
(1)求抛物线的解析式;(2)若PE=5EF,求m的值;(3)若点E′是点E关于直线PC的对称点、是否存在点P,使点E/落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.
(1)求证:△AOE≌△COF;
(2)若∠EOD=30°,求CE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 为锐角,点
为锐角,点 为直线
为直线 上一动点,以
上一动点,以 为直角边且在
为直角边且在 的右侧作等腰直角三角形
的右侧作等腰直角三角形 ,
, ,
, .
.
(1)如果
 ,
, .
.①当点
 在线段
在线段 上时,如图1,线段
上时,如图1,线段 、
、 的位置关系为___________,数量关系为_____________
的位置关系为___________,数量关系为_____________②当点
 在线段
在线段 的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.(2)如图3,如果
 ,
, ,点
,点 在线段
在线段 上运动。探究:当
上运动。探究:当 多少度时,
多少度时, ?小明通过(1)的探究,猜想
?小明通过(1)的探究,猜想 时,
时, .他想过点
.他想过点 做
做 的垂线,与
的垂线,与 的延长线相交,构建图2的基本图案,寻找解决此问题的方法。小明的想法对吗?如不对写出你的结论;如对按此方法解决问题并写出理由.
的延长线相交,构建图2的基本图案,寻找解决此问题的方法。小明的想法对吗?如不对写出你的结论;如对按此方法解决问题并写出理由.
相关试题

