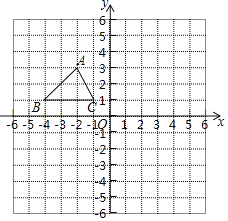
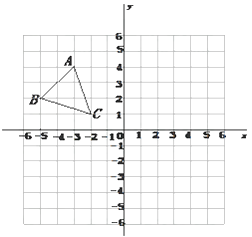
【题目】△ABC在直角坐标系中的位置如图,其中A点的坐标是(﹣2,3)
(1)△ABC绕点O顺时针旋转90°得到△A1B1C1,请作出△A1B1C1,并写出A点的对应点A1的坐标;
(2)若△ABC经过平移后A点的对应点A2的坐标是(2,﹣1),请作△A2B2C2,并计算平移的距离.
参考答案:
【答案】(1)图详见解析,A1的坐标为(3,2);(2)图详见解析,平移的距离为4![]() .
.
【解析】
(1)分别作出三顶点绕点O顺时针旋转90°得到的对应点,再顺次连接即可得;
(2)将三顶点分别向右平移4个单位,再向下平移4个单位得到对应点,继而首顺次连接即可得.
解:(1)分别作出A、B、C绕点O顺时针旋转90°得到的A1、B1、C1,再顺次连接A1B1、A1C1、B1C1如图所示,△A1B1C1即为所求,
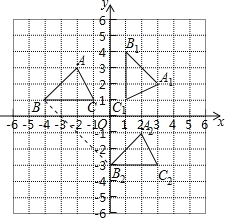
A点的对应点A1的坐标为(3,2);
(2)由点A(﹣2,3)平移到对应点A2(2,﹣1)的平移规律为:向右平移4个单位,再向下平移4个单位
∴将点B和点C也向右平移4个单位,再向下平移4个单位得到B2、C2,连接A2B2、A2C2、B2C2,如图所示,△A2B2C2即为所求,平移的距离AA2=![]() =4
=4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>0.其中正确的结论的个数是( )
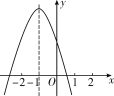
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,
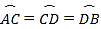 ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )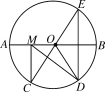
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别 A(-3,4)B(-5,2)C(-2,1)
(1)画出 △ABC关于y 轴的对称图形 △A1B1C1;
(2)画出将△ABC 绕原点 O逆时针方向旋转90°得到的△A2B2C2 ;
(3)求(2)中线段 OA扫过的图形面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂,甲负责加工A型零件,乙负责加工B型零件.已知甲加工60个A型零件所用时间和乙加工80个B型零件所用时间相同,每天甲、乙两人共加工两种零件35个.
(1)求甲、乙每天各加工多少个零件;
(2)根据市场预测估计,加工一个A型零件所获得的利润为35元/件,加工一个B型零件所获得的利润每件比A型少5元,现在需要加工甲、乙两种零件共300个且要求所获得的总利润不低于9850元,求至少应该生产多少个A型零件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
相关试题

