【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
参考答案:
【答案】(1)y=-0.5x+80;(2)10棵;(3)40棵时果园的最大产量是7200千克.
【解析】试题分析:(1)函数的表达式为y=kx+b,把点(12,74),(28,66)代入解方程组即可.(2)列出方程解方程组,再根据实际意义确定x的值.(3)构建二次函数,利用二次函数性质解决问题.
试题解析:(1)设函数的表达式为y=kx+b,该一次函数过点(12,74),(28,66),
得![]() ,
,
解得![]() ,
,
∴该函数的表达式为y=﹣0.5x+80,
(2)根据题意,得,
(﹣0.5x+80)(80+x)=6750,
解得,x1=10,x2=70
∵投入成本最低.
∴x2=70不满足题意,舍去.
∴增种果树10棵时,果园可以收获果实6750千克.
(3)根据题意,得
w=(﹣0.5x+80)(80+x)
=﹣0.5 x2+40 x+6400
=﹣0.5(x﹣40)2+7200
∵a=﹣0.5<0,则抛物线开口向下,函数有最大值
∴当x=40时,w最大值为7200千克.
∴当增种果树40棵时果园的最大产量是7200千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.﹣12﹣8=﹣4
B.﹣5+4=﹣9
C.﹣1﹣9=﹣10
D.﹣32=9 -
科目: 来源: 题型:
查看答案和解析>>【题目】长方形一边的长为3m+2n,与其相邻的另一边的长比它长m-n,则这个长方形的面积是( )
A. 12m2+11mn+2n2 B. 12m2+5mn+2n2
C. 12m2-5mn+2n2 D. 12m2+11mn+n2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.
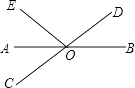
(1)若∠EOC=72°,求∠BOD的度数;
(2)若∠DOE=2∠AOC,判断射线OE,OD的位置关系并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”贯穿欧亚大陆,东边连接亚太经济圈,西边进入欧洲经济圈,大致涉及65个国家,总人口44亿,生产总值23万亿美元.将23万用科学记数法表示应为( )
A. 23×104B. 2.3×105C. 2.3×104D. 0.23×106
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式-6x-4<3x+5的最小整数解是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=40°:

(1)如图(1)BO、CO是△ABC的内角角平分线,且相交于点O,求∠BOC;
(2)如图(2)BO、CO是△ABC的外角角平分线,且相交于点O,求∠BOC;
(3)如图(3)BO、CO分别是△ABC的一内角和一外角角平分线,且相交于点O,求∠BOC;
(4)根据上述三问的结果,当∠A=n°时,分别可以得出∠BOC与∠A有怎样的数量关系(只需写出结论).
相关试题

