【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙O的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
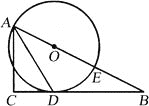
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC=![]() ,求⊙O的半径.
,求⊙O的半径.
参考答案:
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)、连接OD,根据切线的性质以及∠C的度数得出OD∥AC,从而的得出∠CAD=∠ADO,然后根据OA=OD得出∠OAD=∠ADO,从而说明角平分线;(2)、首先根据韦达定理求出AD的长度,连接DE,根据题意得出△ACD和△ADE相似,从而得出AE的长度,然后得出圆的半径.
试题解析:(1)连接OD, ∵BC是⊙O的切线, ∴OD⊥BC ∴∠ODB=90°
又∵∠C=90° ∴AC∥OD ∴∠CAD=∠ADO 又∵OA=OD ∴∠OAD=∠ADO
∴∠CAD=∠OAD ∴ AD平分∠BAC
(2)在Rt△ACD中 AD=![]()
连接DE, ∵AE为⊙O的直径 ∴∠ADE=90° ∴∠ADE=∠C ∵∠CAD=∠OAD
∴△ACD∽△ADE ∴![]() , 即
, 即![]() ∴AE=
∴AE=![]() ∴⊙O的半径是
∴⊙O的半径是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(m+3)x2﹣3m﹣1=0是一元二次方程,则m的取值范围是( )
A.m≠0
B.m≠﹣3
C.m≠3
D.m≠x -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OE,OF分别平分∠AOC,∠BOC,若∠EOF=45°,试判断OA与OB的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若ab=-2,a-3b=5,则a3b-6a2b2+9ab3的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+2|+
 =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3). 
(1)求a,b的值及S△ABC;
(2)若点M在x轴上,且S△ACM= S△ABC , 试求点M的坐标.
S△ABC , 试求点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
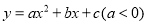 与双曲线
与双曲线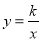 全相交于点A、B,且抛物线经过坐标原点,点
全相交于点A、B,且抛物线经过坐标原点,点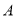 的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.
的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.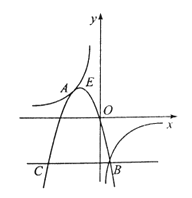
(1)求双曲线和抛物线的解析式;
(2)计算
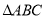 与
与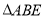 的面积;
的面积;(3)在抛物线上是否存在点D,使
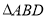 的面积等于
的面积等于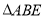 的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.
的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
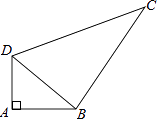
查看答案和解析>>【题目】如图,四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠A=90°,计算四边形ABCD的面积 .
相关试题

