【题目】如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+2|+ ![]() =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3). 
(1)求a,b的值及S△ABC;
(2)若点M在x轴上,且S△ACM= ![]() S△ABC , 试求点M的坐标.
S△ABC , 试求点M的坐标.
参考答案:
【答案】
(1)解:∵|a+2|+ ![]() =0,
=0,
∴a+2=0,b﹣4=0,
∴a=﹣2,b=4,
∴点A(﹣2,0),点B(4,0).
又∵点C(0,3),
∴AB=|﹣2﹣4|=6,CO=3,
∴S△ABC= ![]() ABCO=
ABCO= ![]() ×6×3=9
×6×3=9
(2)解:设点M的坐标为(x,0),则AM=|x﹣(﹣2)|=|x+2|,
又∵S△ACM= ![]() S△ABC,
S△ABC,
∴ ![]() AMOC=
AMOC= ![]() ×9,
×9,
∴ ![]() |x+2|×3=3,
|x+2|×3=3,
∴|x+2|=2,
即x+2=±2,
解得:x=0或﹣4,
故点M的坐标为(0,0)或(﹣4,0)
【解析】(1)由“|a+2|+ ![]() =0”结合绝对值、算术平方根的非负性即可得出a、b的值,再结合三角形的面积公式即可求出S△ABC的值;(2)设出点M的坐标,找出线段AM的长度,根据三角形的面积公式结合S△ACM=
=0”结合绝对值、算术平方根的非负性即可得出a、b的值,再结合三角形的面积公式即可求出S△ABC的值;(2)设出点M的坐标,找出线段AM的长度,根据三角形的面积公式结合S△ACM= ![]() S△ABC , 即可得出AM的值,从而得出点M的坐标.
S△ABC , 即可得出AM的值,从而得出点M的坐标.
【考点精析】本题主要考查了三角形的面积的相关知识点,需要掌握三角形的面积=1/2×底×高才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OE,OF分别平分∠AOC,∠BOC,若∠EOF=45°,试判断OA与OB的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若ab=-2,a-3b=5,则a3b-6a2b2+9ab3的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙O的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
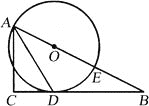
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC=
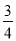 ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
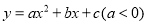 与双曲线
与双曲线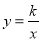 全相交于点A、B,且抛物线经过坐标原点,点
全相交于点A、B,且抛物线经过坐标原点,点 的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.
的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.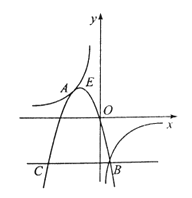
(1)求双曲线和抛物线的解析式;
(2)计算
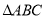 与
与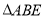 的面积;
的面积;(3)在抛物线上是否存在点D,使
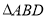 的面积等于
的面积等于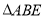 的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.
的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
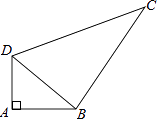
查看答案和解析>>【题目】如图,四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠A=90°,计算四边形ABCD的面积 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若要(a﹣1)a﹣4=1成立,则a=_____.
相关试题

