【题目】如图,四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠A=90°,计算四边形ABCD的面积 . 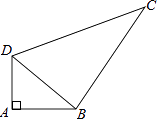
参考答案:
【答案】36
【解析】解:在△ABD中, ∵∠A=90°,AD=3,AB=4,
∴BD= ![]() =5,
=5,
S△ABD= ![]() ABAD=
ABAD= ![]() ×4×3=6,
×4×3=6,
在△BCD中,
∵BC=12,CD=13,BD=5,
∴BD2+BC2=CD2 ,
∴△CBD是直角三角形,
∴S△CBD= ![]() BCBD=
BCBD= ![]() ×12×5=30.
×12×5=30.
∴四边形ABCD的面积=S△ABD+S△BCD=6+30=36.
所以答案是:36.
【考点精析】根据题目的已知条件,利用勾股定理的概念和勾股定理的逆定理的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙O的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
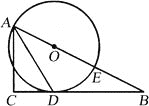
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC=
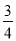 ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+2|+
 =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3). 
(1)求a,b的值及S△ABC;
(2)若点M在x轴上,且S△ACM= S△ABC , 试求点M的坐标.
S△ABC , 试求点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
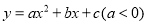 与双曲线
与双曲线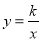 全相交于点A、B,且抛物线经过坐标原点,点
全相交于点A、B,且抛物线经过坐标原点,点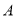 的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.
的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.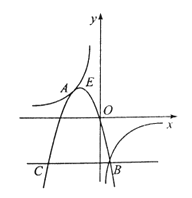
(1)求双曲线和抛物线的解析式;
(2)计算
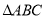 与
与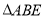 的面积;
的面积;(3)在抛物线上是否存在点D,使
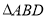 的面积等于
的面积等于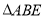 的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.
的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若要(a﹣1)a﹣4=1成立,则a=_____.
-
科目: 来源: 题型:
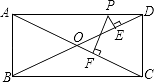
查看答案和解析>>【题目】在矩形ABCD中,已知两邻边AD=12,AB=5,P是AD边上异于A和D的任意一点,且PE⊥BD,PF⊥AC,E、F分别是垂足,那么PE+PF= .
-
科目: 来源: 题型:
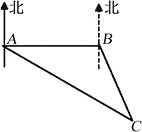
查看答案和解析>>【题目】如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
相关试题

