【题目】如图,已知OE,OF分别平分∠AOC,∠BOC,若∠EOF=45°,试判断OA与OB的位置关系,并说明理由. 
参考答案:
【答案】解:OA⊥OB. 理由如下:∵OE、OF分别平分∠AOC,∠BOC,
∴∠EOC= ![]() ∠AOC∠FOC=
∠AOC∠FOC= ![]() ∠BOC,
∠BOC,
又∵∠EOF=∠EOC﹣∠FOC= ![]() ∠AOC﹣
∠AOC﹣ ![]() ∠BOC=
∠BOC= ![]() (∠AOC﹣∠BOC)=
(∠AOC﹣∠BOC)= ![]() ∠AOB
∠AOB
∴∠AOB=2∠EOF=2×45°=90°
∴OA⊥OB
【解析】利用角平分线的定义得到∠EOC= ![]() ∠AOC∠FOC=
∠AOC∠FOC= ![]() ∠BOC,则可变形出∠EOF=
∠BOC,则可变形出∠EOF= ![]() ∠AOB,于是得到∠AOB=2∠EOF=90°,所以可判断OA⊥OB.
∠AOB,于是得到∠AOB=2∠EOF=90°,所以可判断OA⊥OB.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果+20%表示增加20%,那么﹣6%表示( )
A.增加14%
B.增加6%
C.减少6%
D.减少26% -
科目: 来源: 题型:
查看答案和解析>>【题目】如果x=3m+1,y=2+9m,那么用x的代数式表示y为( )
A. y=2x B. y=x2 C. y=(x﹣1)2+2 D. y=x2+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(m+3)x2﹣3m﹣1=0是一元二次方程,则m的取值范围是( )
A.m≠0
B.m≠﹣3
C.m≠3
D.m≠x -
科目: 来源: 题型:
查看答案和解析>>【题目】若ab=-2,a-3b=5,则a3b-6a2b2+9ab3的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙O的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
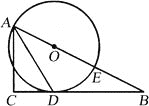
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC=
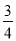 ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+2|+
 =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3). 
(1)求a,b的值及S△ABC;
(2)若点M在x轴上,且S△ACM= S△ABC , 试求点M的坐标.
S△ABC , 试求点M的坐标.
相关试题

