【题目】如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD﹣DO﹣OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).

(1)求点N落在BD上时t的值;
(2)直接写出点O在正方形PQMN内部时t的取值范围;
(3)当点P在折线AD﹣DO上运动时,求S与t之间的函数关系式;
(4)直接写出直线DN平分△BCD面积时t的值.
参考答案:
【答案】(1)![]() ;(2)2<t<
;(2)2<t< ![]() ;(3)见解析; (4)t的值为
;(3)见解析; (4)t的值为 ![]() 、
、 ![]() 、
、 ![]() .
.
【解析】
试题(1)根据条件证明△DPN∽△DQB然后利用对应边成比例得出关于t的方程,解方程即可;(2)只需考虑求出两个临界位置①MN经过点O,②点P与点O重合下t的值即可;(3)①分0<t![]() ,
,![]() <t≤6,6<t≤11三种情况讨论,根据图形面积公式或和差关系即可用t表示出面积s;②因为点P在折线AD-DO运动,所以可分点P在AD上,点P在DO上,两种情况讨论.
<t≤6,6<t≤11三种情况讨论,根据图形面积公式或和差关系即可用t表示出面积s;②因为点P在折线AD-DO运动,所以可分点P在AD上,点P在DO上,两种情况讨论.
试题解析:(1)当点N落在BD上时,
∵四边形PQMN是正方形,∴PN∥QM,PN=PQ=t.
∴△DPN∽△DQB.∴![]() .
.
∵PN=PQ=PA=t,DP=6﹣t,QB=AB=8,∴![]() .∴t=
.∴t=![]()
∴当t=![]() 时,点N落在BD上. (2分)
时,点N落在BD上. (2分)
(2)当点O在正方形PQMN内部时,t的范围是4<t<11(5分)
(3)①当0<t![]() 时,如图4.
时,如图4.

S=S正方形PQMN=PQ2=PA2=t2.
当![]() <t≤6时,如图5,
<t≤6时,如图5,

∵tan∠ADB=![]() =
=![]() ,∴
,∴![]() =
=![]() .∴PG=8﹣
.∴PG=8﹣![]() t.
t.
∴GN=PN﹣PG=t﹣(8﹣![]() t)=
t)=![]() ﹣8.
﹣8.
∵tan∠NFG=tan∠ADB=![]() ,∴
,∴![]() .
.
∴NF=![]() GN=
GN=![]() (
(![]() ﹣8)=
﹣8)=![]() t﹣6.
t﹣6.
∴S=S正方形PQMN﹣S△GNF=t2﹣![]() ×(
×(![]() ﹣8)×(
﹣8)×(![]() t﹣6)
t﹣6)
=﹣![]() t2+14t﹣24.
t2+14t﹣24.
当6<t≤11时,如图6,

∵四边形PQMN是正方形,四边形ABCD是矩形.
∴∠PQM=∠DAB=90°.∴PQ∥AD.∴△BQP∽△BAD.
∴![]() =
=![]() =
=![]() .∵BP=16﹣t,BD=10,BA=8,AD=6,
.∵BP=16﹣t,BD=10,BA=8,AD=6,
∴![]() .∴BQ=
.∴BQ=![]() ,PQ=
,PQ=![]() .
.
∴QM=PQ=![]() .∴BM=BQ﹣QM=
.∴BM=BQ﹣QM=![]() .
.
∵tan∠ABD=![]() ,∴FM=
,∴FM=![]() BM=
BM=![]() .
.
∴S=S梯形PQMF=![]() (PQ+FM)QM=
(PQ+FM)QM=![]() [
[![]() +
+![]() ]
]![]()
=![]() (16﹣t)2=
(16﹣t)2=![]() t2-
t2-![]()
综上所述:当0<t≤![]() 时,S=t2.
时,S=t2.
当![]() <t≤6时,S=﹣
<t≤6时,S=﹣![]() t2+14t﹣24.
t2+14t﹣24.
当6<t≤11时,S=![]() t2-
t2-![]()
②当直线DN平分△BCD面积时,t的值为![]() 、
、![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于D.

(1)求证:∠DBA=∠ABC;
(2)如果BD=1,tan∠BAD=
 ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1﹣x2|+|y1﹣y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
(1)已知O为坐标原点,动点P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(2)设P0(x0,y0)是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离.试求点M(2,1)到直线y=x+2的直角距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形的中心为圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为
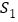 ,
, ,
, ,则
,则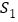 ,
, ,
, 之间的关系是( )
之间的关系是( )
A.
 B.
B. C.
C. D.无法确定
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用(-1,0)表示A点的位置,用(2,1)表示B点的位置,那么:

(1)画出直角坐标系。
(2)写出△DEF的三个顶点的坐标。
(3)在图中表示出点M(6,2),N(4,4)的位置。
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程
已知a、b、c为△ABC为三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状
解:∵a2c2-b2c2=a4-b4①
∴c2(a2-b2)=(a2-b2)(a2+b2)②
∴c2=a2+b2③
∴△ABC是直角三角形
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误?请写出该步的序号________.
(2)错误原因为________.
(3)本题正确结论是什么,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-
 x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.(1)求抛物线y=-x2+bx+c的表达式;
(2)连接GB、EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH、HF,当点E运动到什么位置时,以A、E、F、H为顶点的四边形是矩形?求出此时点E、H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求
 AM+CM的最小值.
AM+CM的最小值.
相关试题

