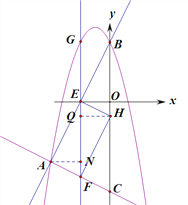
【题目】如图，抛物线y=-x2+bx+c与直线AB交于A(-4，-4)，B(0，4)两点，直线AC：y=-x-6交y轴与点C.点E是直线AB上的动点，过点E作EF⊥x轴交AC于点F，交抛物线于点G.

（1）求抛物线y=-x2+bx+c的表达式；

（2）连接GB、EO，当四边形GEOB是平行四边形时，求点G的坐标；

（3）①在y轴上存在一点H，连接EH、HF，当点E运动到什么位置时，以A、E、F、H为顶点的四边形是矩形？求出此时点E、H的坐标；

②在①的前提下，以点E为圆心，EH长为半径作圆，点M为⊙E上一动点，求AM+CM的最小值.

参考答案：

【答案】（1）y=-x2-2x+4；（2）G(-2，4)；（3）①H(0，-1)；②

【解析】分析：（1）利用待定系数法求出抛物线解析式；

（2）先利用待定系数法求出直线AB的解析式，进而利用平行四边形的对边相等建立方程求解即可；

（3）①先判断出要以点A，E，F，H为顶点的四边形是矩形，只有EF为对角线，利用中点坐标公式建立方程即可；

②先取EG的中点P进而判断出△PEM∽△MEA即可得出PM=AM，连接CP交圆E于M，再求出点P的坐标即可得出结论．

详解：（1）（1）∵点A（-4，-4），B（0，4）在抛物线y=-x2+bx+c上，

∴，

∴，

∴抛物线的解析式为y=-x2-2x+4；

（2）设直线AB的表达式为y=kx+b

∵直线AB过点A(-4，-4)，B(0，4)，

∴，解得，

∴y=2x+4

设E(m，2m+4)，则G(m，-m2-2m+4)

∵四边形GEOB是平行四边形，

∴GE=OB=4，

∴-m2-2m+4-2m-4=4，解得m=-2

∴G(-2，4)

（3）①设E(m，2m+4)，则F(m，-m-6)

过A作AN⊥EG，过H作HQ⊥EG

四边形AFHE是矩形，∴△PFN≌△HEQ，∴AN=QH，∴m+4=-m，解得m=-2，E(-2，0)

EQ=FN=-4+m+6=1

∴H(0，-1)

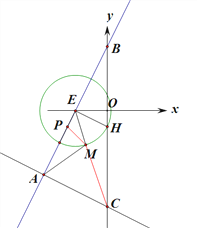
②由题意可得，E(-2，0)，H(0，-1),∴EH=，即⊙E的半径为，

∵M点在⊙E上，∴EM=

∵A(-4，-4)，E(-2，0)，∴AE=2

在AE上截取EP=EM，则EP=，连接PM，

在ΔEPM与ΔEMA中，∵====，∠PEM=∠MEA，∴ΔEPM∽ΔEMA∴PM=AM

∴线段PC的长即为AM+CM的最小值

由EP=EM=AE=×2=，AP=AE-PE= , AC=2 ∴PC=

即AM+CM的最小值为.

关闭