【题目】阅读下列解题过程
已知a、b、c为△ABC为三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状
解:∵a2c2-b2c2=a4-b4①
∴c2(a2-b2)=(a2-b2)(a2+b2)②
∴c2=a2+b2③
∴△ABC是直角三角形
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误?请写出该步的序号________.
(2)错误原因为________.
(3)本题正确结论是什么,并说明理由.
参考答案:
【答案】③ ![]() 有可能为0
有可能为0
【解析】
根据观察可知③不能只是![]() ,若
,若![]() =0,就不会得出③;若
=0,就不会得出③;若![]() ≠0,可得出③;显然,此题需分类讨论.
≠0,可得出③;显然,此题需分类讨论.
(1)③
(2)![]() 有可能为0,
有可能为0,
(3)本题正确结论是:△ABC的形状为等腰三角形或直角三角形,
理由是:由上面解题第②步可知,当a≠b时,c2=a2+b2 ,这时△ABC为直角三角形;
当a=b时,△ABC为等腰三角形,
当a≠b时,△ABC为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A.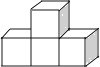
B.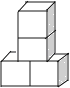
C.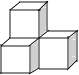
D.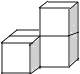
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用(-1,0)表示A点的位置,用(2,1)表示B点的位置,那么:

(1)画出直角坐标系。
(2)写出△DEF的三个顶点的坐标。
(3)在图中表示出点M(6,2),N(4,4)的位置。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过反比例函数y=
 (x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为( )
(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为( ) 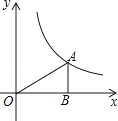
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两名同学在同一个学校上学,B同学上学的路上经过A同学家。A同学步行,B同学骑自行车,某天,A,B两名同学同时从家出发到学校,如图,
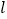 A表示A同学离B同学家的路程
A表示A同学离B同学家的路程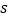 A(m)与行走时间
A(m)与行走时间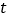 (min)之间的函数关系图象,
(min)之间的函数关系图象,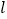 B表示B同学离家的路程
B表示B同学离家的路程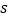 B(m)与行走时间
B(m)与行走时间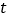 (min)之间的函数关系图象.
(min)之间的函数关系图象.(1)A,B两名同学的家相距________m.
(2)B同学走了一段路后,自行车发生故障,进行修理,修理自行车所用的时间是 _____min.
(3)B同学出发后______min与A同学相遇.
(4)求出A同学离B同学家的路程
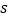 A与时间
A与时间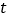 的函数关系式.
的函数关系式.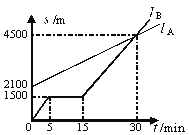
-
科目: 来源: 题型:
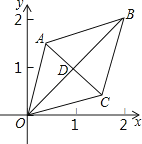
查看答案和解析>>【题目】如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )
A.(1,﹣1)
B.(﹣1,﹣1)
C.(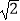 ,0)
,0)
D.(0,﹣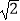 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作
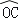 交
交 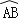 于点C,若OA=2,则阴影部分的面积为 .
于点C,若OA=2,则阴影部分的面积为 . 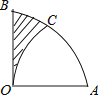
相关试题

