【题目】周末,小明和爸爸在400米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:

(1)他们的对话内容,求小明和爸爸的骑行速度,
(2)一次追上小明后,在第二次相遇前,再经过多少分钟,小明和爸爸相距50m?
参考答案:
【答案】(1)小明骑行速度为200m/分钟,爸爸骑行速度为400m/分钟;(2)爸爸第一次追上小明后,在第二次相遇前,再经过![]() 分或
分或![]() 钟,小明和爸爸相距50m.
钟,小明和爸爸相距50m.
【解析】
(1)设小明的骑行速度为x米/分钟,则爸爸的骑行速度为2x米/分钟,根据距离=速度差×时间即可得出关于x的一元一次方程,解之即可得出结论;
(2)设爸爸第一次追上小明后,在第二次相遇前,再经过y分钟,小明和爸爸跑道上相距50m.分第一次相遇后爸爸比小明多骑50米和350米两种情况考虑,根据距离=速度差×时间即可得出关于y的一元一次方程,解之即可得出结论.
(1)设小明的骑行速度为x米/分钟,则爸爸的骑行速度为2x米/分钟,
根据题意得:2(2x-x)=400,
解得:x=200,
∴2x=400.
答:小明的骑行速度为200米/分钟,爸爸的骑行速度为400米/分钟.
(2)设爸爸第一次追上小明后,在第二次相遇前,再经过y分钟,小明和爸爸跑道上相距50m,
①爸爸第一次追上小明后,在第二次相遇前,爸爸又比小明多骑了50米,
根据题意得:400y-200y=50,
解得:y=![]() ;
;
②爸爸第一次追上小明后,在第二次相遇前,爸爸又比小明多骑了350米,
根据题意得:400y-200y=350,
解得:y=![]() .
.
答:第二次相遇前,再经过![]() 或
或![]() 分钟,小明和爸爸跑道上相距50m.
分钟,小明和爸爸跑道上相距50m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张同学尝试运用课堂上学到的方法,自主研究函数
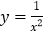 的图像与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
的图像与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:(1)函数y=
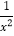 的定义域是 ;
的定义域是 ;(2)下表列出了
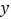 与
与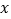 的几组对应值:
的几组对应值: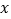
…
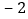
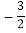
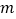
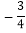
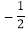

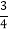
1

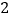
…
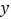
…
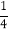

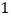
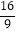
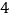
4
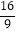
1

…
表中
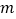 的值是 ;
的值是 ;(3)如图,在平面直角坐标系
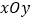 中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图像;
中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图像;(4)结合函数
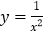 的图像,写出这个函数的性质: .(只需写一个)
的图像,写出这个函数的性质: .(只需写一个)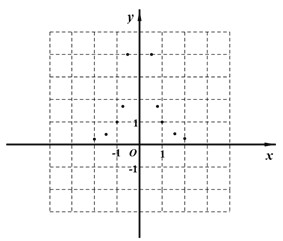
-
科目: 来源: 题型:
查看答案和解析>>【题目】求证:三角形的一条中位线与第三边上的中线互相平分.
要求:(1)根据给出的
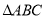 和它的一条中位线
和它的一条中位线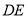 ,在给出的图形上,请用尺规作出
,在给出的图形上,请用尺规作出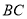 边上的中线
边上的中线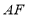 ,交
,交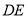 于点
于点 .不写作法,保留痕迹;
.不写作法,保留痕迹;(2)据此写出已知,求证和证明过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】荔枝上市后,某水果店的老板用500元购进第一批荔枝,销售完后,又用800元购进第二批荔枝,所购件数是第一批购进件数的2倍,但每件进价比第一批进价少5元.
(1)求第一批荔枝每件的进价;
(2)若第二批荔枝以30元/件的价格销售,在售出所购件数的
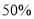 后,为了尽快售完,决定降价销售,要使第二批荔枝的销售利润不少于300元,剩余的荔枝每件售价至少多少元?
后,为了尽快售完,决定降价销售,要使第二批荔枝的销售利润不少于300元,剩余的荔枝每件售价至少多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点A,B表示的有理数分别为﹣6,3,点P是射线AB上一个动点(不与点A,B重合).M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.
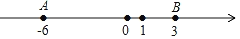
(1)若点P表示的有理数是0,那么MN的长为 ;若点P表示的有理数是6,那么MN的长为 .
(2)点P在射线AB上运动(不与点A,B重合)的过程中,MN的长是否发生改变?若不改变,请写出求MN的长的过程;若改变,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】记Sn=a1+a2+…+an,令Tn=
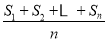 ,称Tn为a1,a2,…,an这列数的“神秘数”.已知a1,a2,…,a500的“神秘数”为1503,那么6,a1,a2,…,a500的“神秘数”为( )
,称Tn为a1,a2,…,an这列数的“神秘数”.已知a1,a2,…,a500的“神秘数”为1503,那么6,a1,a2,…,a500的“神秘数”为( )A.1504B.1506C.1508D.1510
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有20箱苹果,以每箱25千克为标准,超过的千克数用正数表示,不足的千克数用负数表示,结果记录如表:
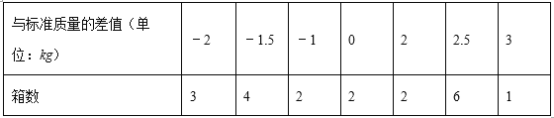
(1)20箱苹果中,最重的一箱比最轻的一箱重 kg;
(2)与标准质量相比,20箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价12元,则售出这20箱苹果可获得多少元?
相关试题

