【题目】求证:三角形的一条中位线与第三边上的中线互相平分.
要求:(1)根据给出的![]() 和它的一条中位线
和它的一条中位线![]() ,在给出的图形上,请用尺规作出
,在给出的图形上,请用尺规作出![]() 边上的中线
边上的中线![]() ,交
,交![]() 于点
于点![]() .不写作法,保留痕迹;
.不写作法,保留痕迹;
(2)据此写出已知,求证和证明过程.

参考答案:
【答案】(1)作线段![]() 的中段线,
的中段线,![]() 的中点为
的中点为![]() ,连结
,连结![]() 即可,见解析;(2) 见解析.
即可,见解析;(2) 见解析.
【解析】
(1)作BC的垂直平分线得到BC的中点F,从而得到BC边上的中线AF;
(2)写出已知、求证,连接DF、EF,如图,先证明EF为AB边的中位线,利用三角形中位线性质得到EF∥AD,EF=AD,则可判断四边形ADFE为平行四边形,从而得到DE与AF互相平分.
解:(1)作线段![]() 的中段线,
的中段线,![]() 的中点为
的中点为![]() ,连结
,连结![]() 即可。
即可。
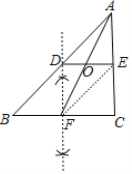
(2)已知:![]() 分别为
分别为![]() 三边
三边![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() 。
。
求证:![]() 与
与![]() 互相平分。
互相平分。
证明:连结![]() ,
,
![]() 分别为
分别为![]() 的中点,
的中点,
有![]() ,
,
又![]() 为
为![]() 中点,
中点,
所以,![]() ,
,
四边形![]() 为平行四边形,
为平行四边形,
所以,![]() 与
与![]() 互相平分.
互相平分.
-
科目: 来源: 题型:
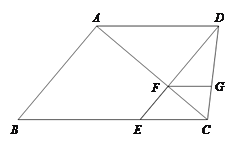
查看答案和解析>>【题目】已知:如图,梯形ABCD中,AD∥BC,DE∥AB,
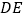 与对角线
与对角线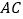 交于点
交于点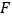 ,
,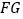 ∥
∥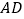 ,且FG=EF.
,且FG=EF.(1)求证:四边形
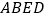 是菱形;
是菱形;(2)联结AE,又知AC⊥ED,求证:
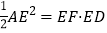 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知射线OA,从O点再引射线OB,OC,使∠AOB=67°31′,∠BOC=48°39′,则∠AOC的度数为_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张同学尝试运用课堂上学到的方法,自主研究函数
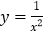 的图像与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
的图像与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:(1)函数y=
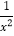 的定义域是 ;
的定义域是 ;(2)下表列出了
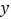 与
与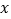 的几组对应值:
的几组对应值: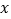
…
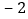
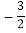
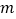
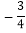
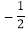

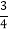
1

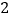
…
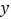
…
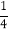

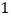
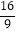
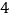
4
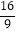
1

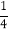
…
表中
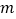 的值是 ;
的值是 ;(3)如图,在平面直角坐标系
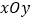 中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图像;
中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图像;(4)结合函数
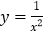 的图像,写出这个函数的性质: .(只需写一个)
的图像,写出这个函数的性质: .(只需写一个)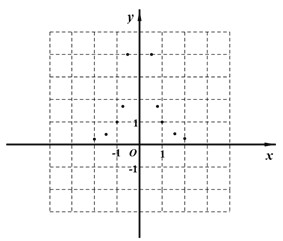
-
科目: 来源: 题型:
查看答案和解析>>【题目】荔枝上市后,某水果店的老板用500元购进第一批荔枝,销售完后,又用800元购进第二批荔枝,所购件数是第一批购进件数的2倍,但每件进价比第一批进价少5元.
(1)求第一批荔枝每件的进价;
(2)若第二批荔枝以30元/件的价格销售,在售出所购件数的
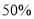 后,为了尽快售完,决定降价销售,要使第二批荔枝的销售利润不少于300元,剩余的荔枝每件售价至少多少元?
后,为了尽快售完,决定降价销售,要使第二批荔枝的销售利润不少于300元,剩余的荔枝每件售价至少多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明和爸爸在400米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:

(1)他们的对话内容,求小明和爸爸的骑行速度,
(2)一次追上小明后,在第二次相遇前,再经过多少分钟,小明和爸爸相距50m?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点A,B表示的有理数分别为﹣6,3,点P是射线AB上一个动点(不与点A,B重合).M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.
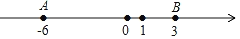
(1)若点P表示的有理数是0,那么MN的长为 ;若点P表示的有理数是6,那么MN的长为 .
(2)点P在射线AB上运动(不与点A,B重合)的过程中,MN的长是否发生改变?若不改变,请写出求MN的长的过程;若改变,请说明理由.
相关试题

