【题目】如图,在Rt△ABC中,已知∠C=90°,sinB=![]() ,AC=8,D为线段BC上一点,CD=2.
,AC=8,D为线段BC上一点,CD=2.
(1)求BD的值;
(2)求cos∠DAC的值.

参考答案:
【答案】(1)BD=4; (2) ![]()
【解析】试题分析:
(1) 由于已知线段CD的长,所以只要求得线段BC的长就容易得到线段BD的长. 已知![]() 的值以及线段AC的长,利用锐角三角函数的定义不难在Rt△ABC中得到线段AB的长,进而通过勾股定理求得线段BC的长.
的值以及线段AC的长,利用锐角三角函数的定义不难在Rt△ABC中得到线段AB的长,进而通过勾股定理求得线段BC的长.
(2) 在Rt△ACD中,由于已知线段AC与CD的长,所以可以通过勾股定理得到线段AD的长. 通过锐角三角函数的定义,可以在Rt△ACD中求得![]() 的值.
的值.
试题解析:
(1) ∵在Rt△ABC中, ![]() ,
,
又∵AC=8,
∴![]() ,
,
∴AB=10,
∴在Rt△ABC中, ![]() ,
,
∵CD=2,
∴BD=BC-CD=6-2=4.
(2) ∵AC=8,CD=2,
∴在Rt△ACD中, ![]() ,
,
∴在Rt△ACD中, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b是等腰△ABC的两边长,且满足a2+b2-8a-4b+20=0,求a、b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自来水公司的收费标准如下:若每户用水不超过5立方米,则每立方米收费2.8元;若每户每月用水超过5立方米,则超出部分每立方米收费3元.小颖家每月水费都不少于29元,小颗家每月用水量至少( )
A. 11立方米B. 10立方米C. 9立方米D. 5立方米
-
科目: 来源: 题型:
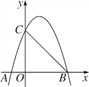
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别交于A(-1,0)、B(3,0)、C(0,3)三点.
(1)试求抛物线的解析式;
(2)P是直线BC上方的抛物线上的一个动点,设P的横坐标为t,P到BC的距离为h,求h与t的函数关系式,并求出h的最大值;
(3)设点M是x轴上的动点,在平面直角坐标系中,是否存在点N,使得以点A、C、M、N为顶点的四边形是菱形?若存在,求出所有符合条件的点N坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】聊城流传着一首家喻户晓的民谣:“东昌府,有三宝,铁塔、古楼、玉皇皋.”被人们誉为三宝之一的铁塔,初建年代在北宋早期,是本市现存最古老的建筑.如图,测绘师在离铁塔10米处的点C测得塔顶A的仰角为α,他又在离铁塔25米处的点D测得塔顶A的仰角为β,若tanαtanβ=1,点D,C,B在同一条直线上,那么测绘师测得铁塔的高度约为(参考数据:
 ≈3.162)( )
≈3.162)( )
A. 15.81米 B. 16.81米 C. 30.62米 D. 31.62米
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:
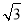 ≈1.732,结果精确到0.1)?
≈1.732,结果精确到0.1)?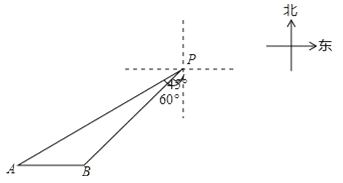
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量出楼房AC的高度,从距离楼底C处
 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈ ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).
相关试题

