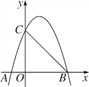
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别交于A(-1,0)、B(3,0)、C(0,3)三点.
(1)试求抛物线的解析式;
(2)P是直线BC上方的抛物线上的一个动点,设P的横坐标为t,P到BC的距离为h,求h与t的函数关系式,并求出h的最大值;
(3)设点M是x轴上的动点,在平面直角坐标系中,是否存在点N,使得以点A、C、M、N为顶点的四边形是菱形?若存在,求出所有符合条件的点N坐标;若不存在,说明理由.
参考答案:
【答案】(1)y=-x2+2x+3.(2) t=![]() 时,最大值为
时,最大值为![]() .(3) 存在.N1(0,-3),N2(-
.(3) 存在.N1(0,-3),N2(-![]() ,3),N3(
,3),N3(![]() ,3),N4(-5,3).
,3),N4(-5,3).
【解析】试题分析:(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线的解析式;
(2)过点P作PD⊥x轴于点D,交BC于点E,PH⊥BC于点H,连结PB、PC,可先求得直线BC的解析式,则可用t分别表示出E的坐标,从而可表示出PE的长,再可用t表示出△PBC的面积,再利用等积法可用t表示出h,利用二次函数的性质可求得h的最大值;
(3)分AM、CM和AC为对角线三种情况,分别根据菱形的性质可求得N点的坐标.
试题解析:(1)∵抛物线y=ax2+bx+c过A(-1,0)、B(3,0)、C(0,3)三点,
∴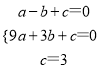 ,解得
,解得 ,
,
∴抛物线的解析式为y=-x2+2x+3;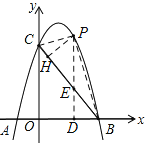
(2)过点P作PD⊥x轴于点D,交BC于点E,PH⊥BC于点H,连结PB、PC.
∵B(3,0)、C(0,3),
∴OB=OC=3,BC=![]() ,
,
设直线BC解析式为y=kx+n,则![]() ,解得
,解得![]()
∴直线BC解析式为y=-x+3,
∵点P的横坐标为t,且在抛物线y=-x2+2x+3上,
∴P(t,-t2+2t+3),
又∵PD⊥x轴于点D,交BC于点E,
∴D(t,0),E(t,-t+3),
∴PE=(-t2+2t+3)-(-t+3)=-t2+3t,
∴S△PBC=S△PEB+S△PEC=![]() PEBD+
PEBD+![]() PEOD=
PEOD=![]() PE(BD+OD)=
PE(BD+OD)=![]() PEOB=
PEOB=![]() (t2+3t)×3=
(t2+3t)×3=![]() t2+
t2+![]() t,
t,
又∵S△PBC=![]() BCPH=
BCPH=![]() ×3
×3![]() h=
h=![]() h,
h,
∴![]() h=
h=![]() t2+
t2+![]() t,
t,
∴h与t的函数关系式为:h=![]() t2+
t2+![]() t(0<t<3),
t(0<t<3),
∵h=![]() t2+
t2+![]() t=
t=![]() (t
(t![]() )2+
)2+![]() ,
,
∴当t=![]() 时,h有最大值为
时,h有最大值为![]() ;
;
(3)存在.
若AM为菱形对角线,则AM与CN互相垂直平分,
∴N(0,-3);
若CM为菱形对角线,则CN=AM=AC=![]() =
=![]() ,
,
∴N(![]() ,3)或N(
,3)或N(![]() ,3);
,3);
若AC为菱形对角线,则CN=AM=CM,
设M(m,0),由CM2=AM2,得m2+32=(m+1)2,解得m=4,
∴CN=AM=CM=5,
∴N(-5,3).
综上可知存在点N,使得以点A、C、M、N为顶点的四边形是菱形,符合条件的点N有4个:N1(0,-3),N2(![]() ,3),N3(
,3),N3(![]() ,3),N4(-5,3).
,3),N4(-5,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学计数法表示为________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b是等腰△ABC的两边长,且满足a2+b2-8a-4b+20=0,求a、b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自来水公司的收费标准如下:若每户用水不超过5立方米,则每立方米收费2.8元;若每户每月用水超过5立方米,则超出部分每立方米收费3元.小颖家每月水费都不少于29元,小颗家每月用水量至少( )
A. 11立方米B. 10立方米C. 9立方米D. 5立方米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,已知∠C=90°,sinB=
 ,AC=8,D为线段BC上一点,CD=2.
,AC=8,D为线段BC上一点,CD=2.(1)求BD的值;
(2)求cos∠DAC的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】聊城流传着一首家喻户晓的民谣:“东昌府,有三宝,铁塔、古楼、玉皇皋.”被人们誉为三宝之一的铁塔,初建年代在北宋早期,是本市现存最古老的建筑.如图,测绘师在离铁塔10米处的点C测得塔顶A的仰角为α,他又在离铁塔25米处的点D测得塔顶A的仰角为β,若tanαtanβ=1,点D,C,B在同一条直线上,那么测绘师测得铁塔的高度约为(参考数据:
 ≈3.162)( )
≈3.162)( )
A. 15.81米 B. 16.81米 C. 30.62米 D. 31.62米
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:
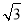 ≈1.732,结果精确到0.1)?
≈1.732,结果精确到0.1)?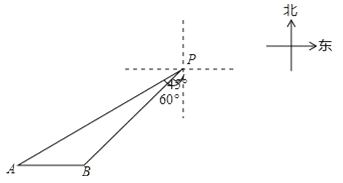
相关试题

