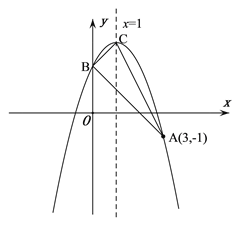
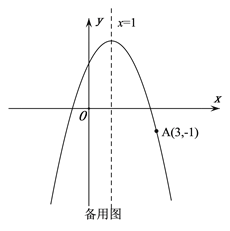
【题目】如图,抛物线![]() 的顶点为C,对称轴为直线
的顶点为C,对称轴为直线![]() ,且经过点A(3,-1),与y轴交于点B.
,且经过点A(3,-1),与y轴交于点B.
(1)求抛物线的解析式;
(2)判断△ABC的形状,并说明理由;
(3)经过点A的直线交抛物线于点P,交x轴于点Q,若![]() ,试求出点P的坐标.
,试求出点P的坐标.
参考答案:
【答案】(1)![]() ;(2)△ABC是直角三角形,理由见解析;(3)点P的坐标为
;(2)△ABC是直角三角形,理由见解析;(3)点P的坐标为![]() 、
、![]() 、
、![]() 或
或![]()
【解析】分析:(1)利用待定系数法,联立方程组即可解得;(2)利用解析式![]() ,可得B(0,2),C(1,3),再由A(3,-1),求出AB,AC,BC ,利用勾股定理的逆定理即可得出结果;(3)分两种情况讨论:当点Q在线段AP上时,当点Q在PA延长线上时,可得点P的坐标.
,可得B(0,2),C(1,3),再由A(3,-1),求出AB,AC,BC ,利用勾股定理的逆定理即可得出结果;(3)分两种情况讨论:当点Q在线段AP上时,当点Q在PA延长线上时,可得点P的坐标.
本题解析:
(1)由题意得: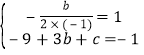 , 解得:
, 解得:![]()
∴抛物线的解析式为![]()
(2)由![]() 得:当
得:当![]() 时,y=2.,∴
时,y=2.,∴![]() ,由
,由![]() 得,
得,![]()
∵A(3,-1),∴![]() ,∴
,∴![]()
∴∠ABC=90°,∴△ABC是直角三角形.
(3)①如图,当点Q在线段AP上时,过点P作PE⊥x轴于点E,AD⊥x轴于点D

∵![]() ,∴PA=2AQ,∴PQ=AQ
,∴PA=2AQ,∴PQ=AQ
∵PE∥AD,∴△PQE∽△AQD,
∴![]() ,∴PE=AD=1
,∴PE=AD=1
由![]() 得:
得:![]()
∴P![]() 或
或![]()
②如图,当点Q在PA延长线上时,过点P作PE⊥x轴于点E,AD⊥x轴于点D
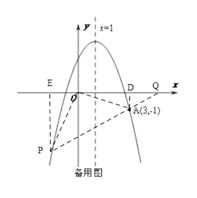
∵![]() ,∴PA=2AQ,∴PQ=3AQ
,∴PA=2AQ,∴PQ=3AQ
∵PE∥AD,∴△PQE∽△AQD,
∴![]() ,∴PE=3AD=3
,∴PE=3AD=3
由![]() 得:
得:![]() ,∴P
,∴P![]() 或
或![]() .
.
综上可知:点P的坐标为![]() 、
、![]() 、
、![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB、AC于点D、E,则以下AE与CE的数量关系正确的是( )

A.AE=
 CEB.AE=
CEB.AE=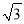 CEC.AE=
CEC.AE=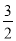 CED.AE=2CE
CED.AE=2CE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.
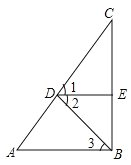
证明:∵ DE⊥BC,AB⊥BC(已知)
∴∠DEC=∠ABC=90°( )
∴DE∥AB(_________ ___)
∴∠2=____ (__________ ___________)
∠1= (____________ _________)
又∵∠1=∠2(_____________________)
∴∠A=∠3(_____________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB:y=﹣x+b分别与x,y轴交于A(6,0)、B 两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
(1)求点B的坐标.
(2)求直线BC的解析式.
(3)直线 EF 的解析式为y=x,直线EF交AB于点E,交BC于点 F,求证:S△EBO=S△FBO.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某天,一蔬菜经营户用90元钱按批发价从蔬菜批发市场买了西红柿和豆角共50kg,然后在市场上按零售价出售,西红柿和豆角当天的批发价和零售价如下表所示:
品名
西红柿
豆角
批发价(单位:元/kg)
2.0
1.5
零售价(单位:元/kg)
2.9
2.6
如果西红柿和豆角全部以零售价售出,他当天卖这些西红柿和豆角赚了多少元钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年6月28日,深湛高铁正式运营.从湛江到广州全程约468km,高铁开通后,运行时间比特快列车所用的时间减少了6h.若高铁列车的平均速度是特快列车平均速度的3倍,求特快列车与高铁的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的扇形统计图和不完整的条形统计图:

请根据以上统计图中的信息解答下列问题.
(1)植树3株的人数为 ;
(2)扇形统计图中植树为1株的扇形圆心角的度数为 ;
(3)该班同学植树株数的中位数是
(4)小明以下方法计算出该班同学平均植树的株数是:(1+2+3+4+5)÷5=3(株),根据你所学的统计知识
判断小明的计算是否正确,若不正确,请写出正确的算式,并计算出结果
相关试题

