搜索
【题目】如图，在△ABC中，∠C=90°，∠A=30°，AB的垂直平分线分别交AB、AC于点D、E，则以下AE与CE的数量关系正确的是（ ）
A.AE=
CEB.AE=
CEC.AE=
CED.AE=2CE
参考答案：
【答案】D
【解析】
首先连接BE，由在△ABC中，∠C=90°，∠A=30°，可求得∠ABC的度数，又由AB的垂直平分线交AB于点D，交AC于点E，根据线段垂直平分线的性质，可得AE=BE，继而可求得∠CBE的度数，然后由含30°角的直角三角形的性质，证得AE=2CE．
连接BE，
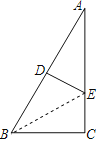
∵DE是AB的垂直平分线，
∴AE=BE，
∴∠ABE=∠A=30°，
∴∠CBE=∠ABC-∠ABE=30°，
在Rt△BCE中，BE=2CE，
∴AE=2CE，
故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】直线上有A，B，C三点，点M是线段AB的中点，点N是线段BC的一个三等分点，如果AB=6，BC=12，求线段MN的长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列两个等式：
，
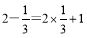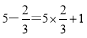，给出定义如下：我们称使等式a﹣b＝ab+1的成立的一对有理数a，b为“共生有理数对”，记为（a，b），如：数对
，
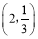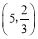，都是“共生有理数对”．（1）数对
，
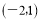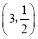中是“共生有理数对”的是 ；（2）若（m，n）是“共生有理数对”，则（﹣n，﹣m） “共生有理数对”（填“是”或“不是”）；
（3）请再写出一对符合条件的“共生有理数对”为 ；（注意：不能与题目中已有的“共生有理数对”重复）
（4）若（a，3）是“共生有理数对”，求a的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在数轴上有A、B、C、D四个点，且线段AB=4，CD=6，已知A表示的数是﹣10，C表示的数是8，若线段AB以每秒6个单位长度的速度，线段CD以每秒2个单位长度的速度在数轴上运动（A在B左侧，C在D左侧）
（1）B，D两点所表示的数分别是 、 ；
（2）若线段AB向右运动，同时线段CD向左运动，经过多少秒时，BC=2；
（3）若线段AB、CD同时向右运动，同时点P从原点出发以每秒1个单位长度的速度向右运动，经过多少秒时，点P到点A，C的距离相等？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠1＝∠2，DE⊥BC，AB⊥BC，求证：∠A＝∠3.
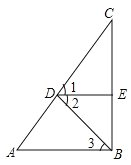
证明：∵ DE⊥BC，AB⊥BC(已知)
∴∠DEC=∠ABC=90°( )
∴DE∥AB（_________ ___）
∴∠2=____ (__________ ___________)
∠1＝ (____________ _________)
又∵∠1＝∠2(_____________________)
∴∠A＝∠3(_____________________)
-
科目： 来源： 题型：
查看答案和解析>>【题目】直线AB：y=﹣x+b分别与x，y轴交于A（6，0）、B 两点，过点B的直线交x轴负半轴于C，且OB：OC=3：1．
(1)求点B的坐标．
(2)求直线BC的解析式．
(3)直线 EF 的解析式为y=x，直线EF交AB于点E，交BC于点 F，求证：S△EBO=S△FBO．
-
科目： 来源： 题型：
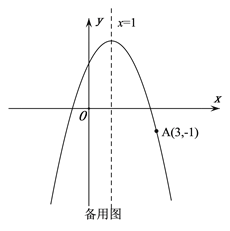
查看答案和解析>>【题目】如图，抛物线
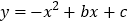的顶点为C，对称轴为直线
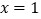，且经过点A(3,－1)，与y轴交于点B.（1）求抛物线的解析式；
（2）判断△ABC的形状，并说明理由；
（3）经过点A的直线交抛物线于点P，交x轴于点Q，若
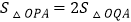，试求出点P的坐标.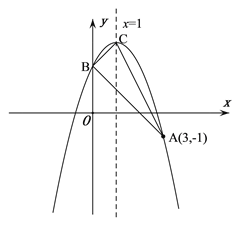
相关试题
