【题目】星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(立方米)与时间x(小时)的函数关系如图所示.
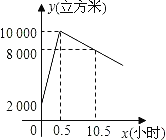
(1)8:00~8:30,燃气公司向储气罐注入了多少立方米的天然气;
(2)当x≥0.5时,求储气罐中的储气量y(立方米)与时间x(小时)的函数解析式;
(3)请你判断,正在排队等候的第18辆车能否在当天10:30之前加完气?请说明理由.
参考答案:
【答案】(1)8000立方米;(2)y=﹣200x+10100.(3)可以,见解析
【解析】
试题分析:(1)由图象可知,加气站原来有2000方气,加气结束后变为10000方,由此即可求出注入了多少方天然气;
(2)x≥0.5时,可设y=kx+b,由图象知,该直线过点(0.5,10000),(10.5,8000),利用方程组即可求解;
(3)第18辆车在10:30之前能否加完气,就要看前18辆车加气所用时间是否超过2小时即可.
解:(1)由图可知,星期天当日注入了10000﹣2000=8000立方米的天然气;(2分)
(2)当x≥0.5时,设储气罐中的储气量y(立方米)与时间x(小时)的函数解析式为:y=kx+b(k,b为常数,且k≠0),
∵它的图象过点(0.5,10000),(10.5,8000),
∴![]() ,
,
解得![]() .
.
故所求函数解析式为:y=﹣200x+10100.(6分)
(3)可以.
∵给18辆车加气需18×20=360(立方米),储气量为10000﹣360=9640(立方米),
于是有:9640=﹣200x+10100,
解得:x=2.3,
2.3﹣0.5=1.8(小时)
而从8:30到10:30相差2.0小时,显然有:1.8<2.0.
故第18辆车在当天10:30之前能加完气.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=
 (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 . 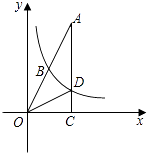
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知当x1=a,x2=b,x3=c时,二次函数y=
 x2+mx对应的函数值分别为y1 , y2 , y3 , 若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3 , 则实数m的取值范围是 .
x2+mx对应的函数值分别为y1 , y2 , y3 , 若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3 , 则实数m的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第
 个图中正方形和等边三角形的个数之和为 个.
个图中正方形和等边三角形的个数之和为 个. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l:y=﹣x+4,在直线l上取点B1,过B1分别向x轴,y轴作垂线,交x轴于A1,交y轴于C1,使四边形OA1B1C1为正方形;在直线l上取点B2,过B2分别向x轴,A1B1作垂线,交x轴于A2,交A1B1于C2,使四边形A1A2B2C2为正方形;按此方法在直线l上顺次取点B3,B4,…,Bn,依次作正方形A2A3B3C3,A3A4B4C4,…,An﹣1AnBnCn,则A3的坐标为___,B5的坐标为___.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).

(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知2014年3月份在某医院出生的20名新生婴儿的体重如下(单位:kg)
4.7 2.9 3.2 3.5 3.8 3.4 2.8 3.3 4.0 4.5
3.6 4.8 4.3 3.6 3.4 3.5 3.6 3.5 3.7 3.7
(1)求这组数据的极差;
(2)若以0.4kg为组距,对这组数据进行分组,制作了如下的“某医院2014年3月份20名新生婴儿体重的频数分布表”(部分空格未填),请在频数分布表的空格中填写相关的量
某医院2014年3月份20名新生儿体重的频数分布表组别(kg)
划记
频数
略
略
3.55﹣3.95
正一
6
略
略
略
合计
20
(3)经检测,这20名婴儿的血型的扇形统计图如图所示(不完整),求:
①这20名婴儿中是A型血的人数;
②表示O型血的扇形的圆心角度数.
相关试题

