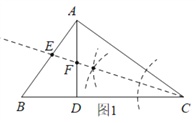
【题目】如图,AD是Rt△ABC斜边BC上的高.
(1)尺规作图:作∠C的平分线,交AB于点E,交AD于点F(不写作法,必须保留作图痕迹,标上应有的字母);
(2)在(1)的条件下,过F画BC的平行线交AC于点H,线段FH与线段CH的数量关系如何?请予以证明;
(3)在(2)的条件下,连结DEDH.求证:ED⊥HD.

参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】分析:
(1)按作角的平分线的尺规作图方法作出相应的图形,并标上相应的字母即可;
(2)如图2,由已知条件易得∠1=∠2,∠1=∠3,从而可得∠2=∠3,由此即可得到FH=CH;
(3)如图3,由已知条件易证∠4=∠5,从而可得AE=AF,由FH∥CD可得△AFH∽△ADC,由此可得![]() 结合FH=CH,AE=AF可得
结合FH=CH,AE=AF可得![]() ,再证∠EAD=∠HCD,即可得到△EAD∽△HCD,从而可得∠7=∠8,结合AD⊥BC即可得到∠EDH=90°,由此即可得到DE⊥DH.
,再证∠EAD=∠HCD,即可得到△EAD∽△HCD,从而可得∠7=∠8,结合AD⊥BC即可得到∠EDH=90°,由此即可得到DE⊥DH.
详解:
(1)如下图1所示,线段CE为所求的△ABC的角平分线;
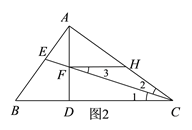
(2)FH=CH,理由如下:
如图2,∵FH∥BC,
∴∠1=∠3,
∵CE平分∠ACB,
∴∠1=∠2,
∴∠2=∠3,
∴FH=CH(等角对等边);
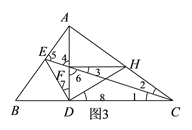
(3)如图3,∵EA⊥CA,
∴∠EAC=90°,
∴∠2+∠5=90°,
∵AD⊥DC,
∴∠ADC=90°,
∴∠1+∠6=90°,
∴∠2+∠5=∠1+∠6,
又∵∠1=∠2,
∴∠5=∠6,
∵∠6=∠4,
∴∠5=∠4,
∴AE=AF(等角对等边),
∵FH∥BC,
∴AFH∽△ADC,
∴![]() =
=![]() ,
,
∵FH=CH,
∴得![]() =
=![]() ,
,
∵∠EAD+∠DAC=90°,∠HCD+∠DAC=90°,
∴∠EAD=∠HCD,
∴△EAD∽△HCD(两边对应成比例且夹角相等的两个三角形相似),
∴∠7=∠8,
∵∠8+∠HDA=90°,
∴∠7+∠HDA=90°,即∠EDH=90°,
∴ED⊥HD
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明学习电学知识后,用四个开关按键(每个开关按键闭合的可能性相等)、一个电源和一个灯泡设计了一个电路图
(1)若小明设计的电路图如图1(四个开关按键都处于打开状态)如图所示,求任意闭合一个开关按键,灯泡能发光的概率;

(2)若小明设计的电路图如图2(四个开关按键都处于打开状态)如图所示,求同时时闭合其中的两个开关按键,灯泡能发光的概率.(用列表或树状图法)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(a,0),B(0,b),且a、b满足
 .
.
(1)填空:a= ,b= ;
(2)如图1,将ΔAOB沿x轴翻折得ΔAOC,D为线段AB上一动点,OE⊥OD交AC于点E,求S四边形ODAE.
(3)如图2,D为AB上一点,过点B作BF⊥OD于点G,交x轴于点F,点H为x轴正半轴上一点,∠BFO=∠DHO,求证:AF=OH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知:点A(0,0),B(
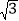 ,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第
,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第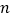 个等边三角形的边长等于__________.
个等边三角形的边长等于__________.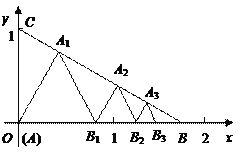
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC边上的中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:①AE=CF;②EF=AP;③2S四边形AEPF=S△ABC;④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合)有BE+CF=EF;上述结论中始终正确的序号有( )个
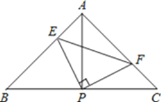
A.1个B.2个C.3个D.4个
相关试题

