【题目】已知A(a,0),B(0,b),且a、b满足![]() .
.

(1)填空:a= ,b= ;
(2)如图1,将ΔAOB沿x轴翻折得ΔAOC,D为线段AB上一动点,OE⊥OD交AC于点E,求S四边形ODAE.
(3)如图2,D为AB上一点,过点B作BF⊥OD于点G,交x轴于点F,点H为x轴正半轴上一点,∠BFO=∠DHO,求证:AF=OH.
参考答案:
【答案】(1))a= -3,b= 3;(2)详见解析
【解析】
(1)根据二次根式和绝对值的非负性列方程组可得a、b的值;
(2)只要证明∴△OBD≌△OAE(ASA),即可推出S四边形ODAE.=![]() ;
;
(3)如图3中,过点O作OP平分∠AOB交BF于P.想办法证明△BOP≌△OAD(ASA),推出OP=AD,再证明△PFO≌△DHA(AAS)即可解决问题.
解:(1)∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
(2)∵A(-3,0),B(0,3),
∴OA=OB=3.
∵ΔAOB沿x轴翻折得ΔAOB,
∴OA=OB=OC,∠AOB=∠AOC=90°,
∴∠ABO=∠BAO=∠CAO=45°,
又∵OE⊥OD,
∴∠BOD=∠AOE,
∵∠DBO=∠EAO,OB=OA,∠BOD=∠AOE,
∴△BOD≌△AOE(ASA),
∴SΔAOE=SΔBOD,
∴S四边形ODAE=![]() =4.5.
=4.5.
(3)过点O作OP平分∠AOB交BF于P,
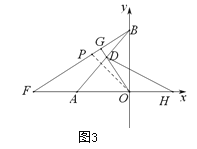
∵OP平分∠AOB且OA=OB,
∴∠AOP=∠BOP=45°,
∵BG⊥OD,
∴∠OBP+∠BOG=90°,
又∵∠AOD+∠BOG=90°,
∴∠OBP=∠AOD,
∵OB=OA,
∴△BOP≌△OAD(ASA)
∴OP=AD,
又∵∠PFO=∠DHO,∠FOP=∠HAD=45°,
∴△PFO≌△DHA(AAS),
∴OF=AH,
∴AF=OH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形DEBF是矩形;
(2)若AF平分∠DAB,AE=3,BF=4,求□ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明学习电学知识后,用四个开关按键(每个开关按键闭合的可能性相等)、一个电源和一个灯泡设计了一个电路图
(1)若小明设计的电路图如图1(四个开关按键都处于打开状态)如图所示,求任意闭合一个开关按键,灯泡能发光的概率;

(2)若小明设计的电路图如图2(四个开关按键都处于打开状态)如图所示,求同时时闭合其中的两个开关按键,灯泡能发光的概率.(用列表或树状图法)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是Rt△ABC斜边BC上的高.
(1)尺规作图:作∠C的平分线,交AB于点E,交AD于点F(不写作法,必须保留作图痕迹,标上应有的字母);
(2)在(1)的条件下,过F画BC的平行线交AC于点H,线段FH与线段CH的数量关系如何?请予以证明;
(3)在(2)的条件下,连结DEDH.求证:ED⊥HD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知:点A(0,0),B(
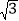 ,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第
,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第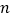 个等边三角形的边长等于__________.
个等边三角形的边长等于__________.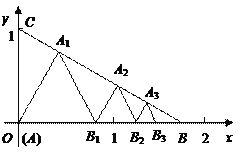
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.

相关试题

