【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
参考答案:
【答案】(1)12万元和10万元.(2)有6种购买方案.
(3)最省钱的购买方案为,选购甲型设备4台,乙型设备6台
【解析】试题分析:(1)设甲,乙两种型号设备每台的价格分别为![]() 万元和
万元和![]() 万元,根据购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.列出方程组,求出
万元,根据购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.列出方程组,求出![]() 的值即可得出答案;
的值即可得出答案;
(2)设节省能源的新设备甲型设备![]() 台,乙型设备
台,乙型设备![]() 台,根据该公司购买节能设备的资金不超过110万元,列出不等式,求出
台,根据该公司购买节能设备的资金不超过110万元,列出不等式,求出![]() 的值即可得出答案;
的值即可得出答案;
(3)因为公司要求每月的产量不低于2040吨,得出![]() 解之求出
解之求出![]() 的值,确定出方案,然后进行比较即可.
的值,确定出方案,然后进行比较即可.
试题解析:(1)设甲,乙两种型号设备每台的价格分别为![]() 万元和
万元和![]() 万元,
万元,
由题意得: ![]() 解得
解得![]()
∴甲,乙两种型号设备每台的价格分别为12万元和10万元.
(2)设购买甲型设备![]() 台,乙型设备
台,乙型设备![]() 台,
台,
则: ![]()
![]()
∵![]() 取非负整数
取非负整数
∴![]() =0,1,2,3,4,5,
=0,1,2,3,4,5,
∴ 有6种购买方案.
![]() 由题意:
由题意: ![]()
∴![]()
∴![]() 为4或5.
为4或5.
当![]() =4时,购买资金为:12×4+10×6=108(万元),
=4时,购买资金为:12×4+10×6=108(万元),
当![]() =5时,购买资金为:12×5+10×5=110(万元),
=5时,购买资金为:12×5+10×5=110(万元),
∴最省钱的购买方案为,选购甲型设备4台,乙型设备6台
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC中,A(1,0),C(0,2),双曲线y=
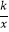 (0<k<2)的图象分别交AB,CB于点E,F,连接OE,OF,EF,S△OEF=2S△BEF , 则k值为( )
(0<k<2)的图象分别交AB,CB于点E,F,连接OE,OF,EF,S△OEF=2S△BEF , 则k值为( )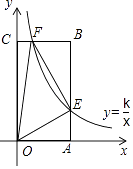
A.
B.1
C.
D.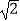
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )

A.40B.24C.20D.15
-
科目: 来源: 题型:
查看答案和解析>>【题目】请把下面证明过程补充完整:
已知:如图,∠ADC=∠ABC,BE、DF分别平行∠ABC、∠ADC,且∠1=∠2.
求证:∠A=∠C.
证明:因为BE、DF分别平分∠ABC、∠ADC,( ).
所以∠1=
 ∠ABC,∠3=
∠ABC,∠3= ∠ADC( ).
∠ADC( ).因为∠ABC=∠ADC(已知),
所以∠1=∠3( ),
因为∠1=∠2(已知),
所以∠2=∠3( ).
所以 ∥ ( ).
所以∠A+∠ =180°,∠C+∠ =180°( ).
所以∠A=∠C( ).

-
科目: 来源: 题型:
查看答案和解析>>【题目】用两种正多边形铺满地面,其中一种是正八边形,则另一种正多边形是( )。
A. 正三角形 B. 正四边形 C. 正五边形 D. 正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=450;③CE=2DE;④AG∥CF;⑤S△FGC=
 .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(﹣4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y=
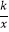 (k>0,x>0)的图象经过点C,则k的值为( )
(k>0,x>0)的图象经过点C,则k的值为( )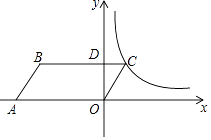
A.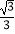
B.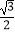
C.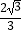
D.
相关试题

