【题目】如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.

参考答案:
【答案】(1)坡底C点到大楼距离AC的值为20![]() 米;(2)斜坡CD的长度为80
米;(2)斜坡CD的长度为80![]() -120米.
-120米.
【解析】(1)在直角三角形ABC中,利用锐角三角函数定义求出AC的长即可;
(2)过点D作DF⊥AB于点F,则四边形AEDF为矩形,得AF=DE,DF=AE.利用DF=AE=AC+CE求解即可.
(1)在直角△ABC中,∠BAC=90°,∠BCA=60°,AB=60米,则AC=![]() (米)
(米)
答:坡底C点到大楼距离AC的值是20![]() 米.
米.
(2)过点D作DF⊥AB于点F,则四边形AEDF为矩形,
∴AF=DE,DF=AE.
设CD=x米,在Rt△CDE中,DE=![]() x米,CE=
x米,CE=![]() x米
x米
在Rt△BDF中,∠BDF=45°,
∴BF=DF=AB-AF=60-![]() x(米)
x(米)
∵DF=AE=AC+CE,
∴20![]() +
+![]() x=60-
x=60-![]() x
x
解得:x=80![]() -120(米)
-120(米)
故斜坡CD的长度为(80![]() -120)米.
-120)米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标:A′ ; B′ ;C′ ;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(4)求△ABC的面积.
-
科目: 来源: 题型:
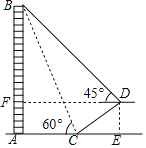
查看答案和解析>>【题目】如图,在等腰△ABC中,
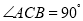 ,
,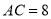 ,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持
,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持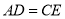 ,连接DE、DF、EF在此运动变化的过程中,下列结论:(1)
,连接DE、DF、EF在此运动变化的过程中,下列结论:(1)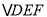 是等腰直角三角形;
是等腰直角三角形;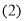 四边形CDFE不可能为正方形,(3)
四边形CDFE不可能为正方形,(3)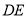 长度的最小值为4;(4)连接CF,CF恰好把四边形CDFE的面积分成1:2两部分,则
长度的最小值为4;(4)连接CF,CF恰好把四边形CDFE的面积分成1:2两部分,则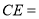
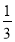 或
或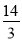 其中正确的结论个数是
其中正确的结论个数是 
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】小林在某商店购买商品A,B共三次,只有其中一次购买时,商品A,B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如表所示,
购买商品A的数量/个
购买商品B的数量/个
购买总费用/元
第一次购物
6
5
1140
第二次购物
3
7
1110
第三次购物
9
8
1062
(1)在这三次购物中,第 次购物打了折扣;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l:y=kx+1与抛物线y=x2-4x
(1)求证:直线l与该抛物线总有两个交点;
(2)设直线l与该抛物线两交点为A,B,O为原点,当k=-2时,求△OAB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在平面直角坐标系中,已知点A(m,0),B(n,0),且m,n满足(m+1)2+
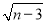 =0,将线段AB向右平移1个单位长度,再向上平移2个单位长度,得到线段CD,其中点C与点A对应,点D与点B对应,连接AC,BD.
=0,将线段AB向右平移1个单位长度,再向上平移2个单位长度,得到线段CD,其中点C与点A对应,点D与点B对应,连接AC,BD.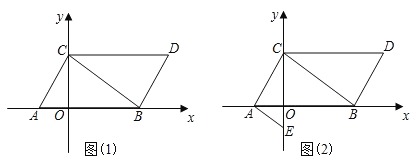
(1)求点A、B、C、D的坐标;
(2)在x轴上是否存在点P,使三角形PBC的面积等于平行四边形ABDC的面积?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),点E在y轴的负半轴上,且∠BAE=∠DCB.求证:AE∥BC.
相关试题

