【题目】如图(1),在平面直角坐标系中,已知点A(m,0),B(n,0),且m,n满足(m+1)2+![]() =0,将线段AB向右平移1个单位长度,再向上平移2个单位长度,得到线段CD,其中点C与点A对应,点D与点B对应,连接AC,BD.
=0,将线段AB向右平移1个单位长度,再向上平移2个单位长度,得到线段CD,其中点C与点A对应,点D与点B对应,连接AC,BD.
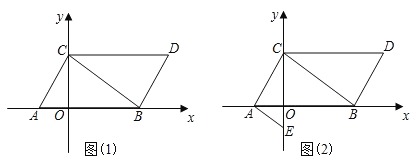
(1)求点A、B、C、D的坐标;
(2)在x轴上是否存在点P,使三角形PBC的面积等于平行四边形ABDC的面积?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),点E在y轴的负半轴上,且∠BAE=∠DCB.求证:AE∥BC.
参考答案:
【答案】(1)A(﹣1,0),B(3,0),C(0,2),D(4,2);(2)存在,点P的坐标为(11,0)或(﹣5,0);(3)见解析.
【解析】
(1)由非负数的性质得出![]() ,且
,且![]() ,求出
,求出![]() ,
,![]() ,得出
,得出![]() ,
,![]() ,由平移的性质得
,由平移的性质得![]() ,
,![]() ;
;
(2)设![]() ,由(1)得
,由(1)得![]() ,
,![]() ,则
,则![]() ,由
,由![]() 得出
得出![]() ,解得
,解得![]() ,或
,或![]() ,即可得出答案;
,即可得出答案;
(3)由平移的性质得![]() ,由平行线的性质得出
,由平行线的性质得出![]() ,证出
,证出![]() ,即可得出结论.
,即可得出结论.
(1)解:∵m,n满足(m+1)2+![]() =0,
=0,
∴m+1=0,且n﹣3=0,
∴m=﹣1,n=3,
∴A(﹣1,0),B(3,0),
由平移的性质得:C(0,2),D(4,2);
(2)解:存在,理由如下:
设P(x,0),
由(1)得:AB=4,OC=2,
∴S平行四边形ABDC=4×2=8,
∵PB=|x﹣3|,
∴S△PBC=![]() PB×OC=
PB×OC=![]() |x﹣3|×2=8,
|x﹣3|×2=8,
解得:x=11,或x=﹣5,
∴点P的坐标为(11,0)或(﹣5,0);
(3)证明:由平移的性质得:AB∥CD,
∴∠DCB=∠CBA,
∵∠BAE=∠DCB,
∴∠BAE=∠CBA,
∴AE∥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l:y=kx+1与抛物线y=x2-4x
(1)求证:直线l与该抛物线总有两个交点;
(2)设直线l与该抛物线两交点为A,B,O为原点,当k=-2时,求△OAB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了节约生活用水,计划制定每位居民统一的月用水量标准,然后根据标准,实行分段收费.为此,对居民上年度的月均用水量进行了抽样调查,并根据调查结果绘制了上年度月均用水量的频数分布直方图(图中分组含最低值,不含最高值),请根据图中信息解答下列问题:
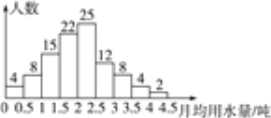
(1)本次调查的居民人数为__________人;
(2)本次调查的居民月均用水量的中位数落在频数分布直方图中的第__________小组内(从左至右数);
(3)当地政府希望让85%左右居民的月均用水量低于制定的月用水量标准,根据上述调查结果,你认为月用水量标准(取整数)定为多少吨时较为合适?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知□ABCD中,A(1,3), B(2,-1), C(5,-5)
(1)D的坐标为____________.
(2)若经过原点的一条直线平分□ABCD的面积,求此直线的解析式
-
科目: 来源: 题型:
查看答案和解析>>【题目】两辆汽车沿同一条路赶赴距离
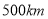 的某景区.甲匀速行驶一段时间出现故障,停车检修后继续行驶.图中折线
的某景区.甲匀速行驶一段时间出现故障,停车检修后继续行驶.图中折线 、线段
、线段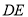 分别表示甲、乙两车所行的路程
分别表示甲、乙两车所行的路程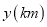 与甲车出发时间
与甲车出发时间 之间的关系,则下列结论中正确的个数是( )①甲车比乙车早出发2小时;②图中的
之间的关系,则下列结论中正确的个数是( )①甲车比乙车早出发2小时;②图中的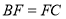 ;③两车相遇时距离目的地
;③两车相遇时距离目的地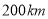 ;④乙车的平均速度是
;④乙车的平均速度是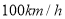 ;⑤甲车检修后的平均速度是
;⑤甲车检修后的平均速度是 .
.
A.1B.2C.3D.4
相关试题

