【题目】如图,直线 AB与坐标轴交与点![]() , 动点P沿路线
, 动点P沿路线![]() 运动.
运动.

(1)求直线AB的表达式;
(2)当点P在OB上,使得AP平分![]() 时,求此时点P的坐标;
时,求此时点P的坐标;
参考答案:
【答案】(1)y=![]() x+6;(2)P(3,0).
x+6;(2)P(3,0).
【解析】
1)直接利用待定系数法即可得出结论;
(2)方法1、利用角平分线判断出BC=AB=10,进而判断出△AOP∽△CBP,求出OP,即可得出结论;
方法2、先判断出OP=PM,设OP=m,得出PM=m,BP=8-m,再求出AM=OA=6,进而得出BM=AB-AM=4,最后用勾股定理建立方程求解即可得出结论.
解:(1)设直线AB的解析式为y=kx+b,
∵A(0,6),B(8,0),
∴![]() ,
,
∴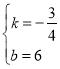 ,
,
∴直线AB的解析式为y=![]() x+6;
x+6;
(2)方法1、如图1,
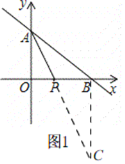
∵A(0,6),B(8,0),
∴OA=6,OB=8,AB=10,
过点B作BC∥OA交AP的延长线于C,
∴∠C=∠OAP,
∵AP平分∠OAB,
∴∠OAP=∠BAP,
∴∠C=∠BAP,
∴BC=AB=10,
∵BC∥OA,
∴△AOP∽△CBP,
∴![]() =
=![]() ,
,
∴![]() ,
,
∴OP=3,
∴P(3,0);
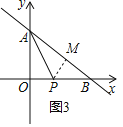
方法2、如图3,过点P作PM⊥AB于M,
∵AP是∠OAB的角平分线,
∴OP=PM,
设OP=m,
∴PM=m,
∴BP=OB-OP=8-m
易知,△AOP≌△AMP,
∴AM=OA=6,
∴BM=AB-AM=4,
在Rt△BMP中,根据勾股定理得,m2+16=(8-m)2,
∴m=3,
∴P(3,0).
故答案为:(1)y=![]() x+6;(2)P(3,0).
x+6;(2)P(3,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:

(1)乙队开挖到30m时,用了_____ h. 开挖6h时甲队比乙队多挖了____ m;
(2)请你求出:
①甲队在
 的时段内,y与x之间的函数关系式;
的时段内,y与x之间的函数关系式;②乙队在
 的时段内,y与x之间的函数关系式;
的时段内,y与x之间的函数关系式;(3)当x 为何值时,甲、 乙两队在 施工过程中所挖河渠的长度相等?
-
科目: 来源: 题型:
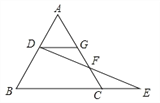
查看答案和解析>>【题目】已知:如图,点D在等边△ABC的边AB上,作DG∥BC,交AC于点G,点F在边AC上,连接DF并延长,交BC的延长线于点E,FE=FD.求证:AD=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
 ,作射线
,作射线 ,再分别作上
,再分别作上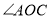 和
和 的平分线
的平分线 、
、 .
.(1) 如图①,当
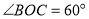 时,求
时,求 的度数;
的度数;(2) 如图②,当射线
 在
在 内绕
内绕 点旋转时,
点旋转时, 的大小是否发生变化,说明理由.
的大小是否发生变化,说明理由.(3) 当射线
 在
在 外绕
外绕 点旋转且
点旋转且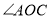 为钝角时,画出图形,请直接写出相应的
为钝角时,画出图形,请直接写出相应的 的度数(不必写出过程) .
的度数(不必写出过程) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】放置在水平桌面上的台灯的灯臂AB长为40 cm,灯罩BC长为30 cm,底座厚度为2 cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少厘米?(结果精确到0.1 cm,参考数据:
 ≈1.732)
≈1.732)

-
科目: 来源: 题型:
查看答案和解析>>【题目】今年我国和俄罗斯联合军事演习中,一核潜艇在海下时而上升,时而下降.核潜艇的初始位置在海平面下500米,下面是核潜艇在某段时间内运动情况(把上升记为“+”下降记为“﹣”,单位:米):﹣280,﹣50,40,30,﹣40,75,﹣55
(1)现在核潜艇处在什么位置(海平面下多少米)?
(2)假如核潜艇每上升或下降1米核动力装置所提供的能量相当于20升汽油燃烧所产生的能量,那么在这一时刻内核动力装置所提供的能量相当于多少升汽油燃烧所产生的能量?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明买了张100元的乘车IC卡,如果他乘车的次数用x表示,则记录他每次乘车后的余额y元)如表:
次数x
1
2
3
4
…
余额y
100-1.2
100-2.4
100-3.6
100-4.8
…
(1)写出乘车的次数x表示余额y的关系式.
(2)利用上述关系式计算小明乘了15次车还剩下多少元?
(3)余额还有40元时,小明已使用此卡乘车多少次?
(4)小强最多能乘几次车?
相关试题

