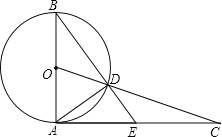
【题目】如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD.
(1)求证:△CDE∽△CAD;
(2)若AB=2,AC=![]() ,求AE的长.
,求AE的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)根据圆周角定理由AB是⊙O的直径得到∠ADB=90°,则∠B+∠BAD=90°,再根据切线的性质,由AC为⊙O的切线得∠BAD+∠CAD=90°,则∠B=∠CAD,由于∠B=∠ODB,∠ODB=∠CDE,所以∠B=∠CDE,则∠CAD=∠CDE,加上∠ECD=∠DCA,根据三角形相似的判定方法即可得到△CDE∽△CAD;
(2)在Rt△AOC中,OA=1,AC=![]() ,根据勾股定理可计算出OC=3,则CD=OC﹣OD=2,然后利用△CDE∽△CAD,根据相似比可计算出CE,再由AE=AC﹣CE可得AE的值.
,根据勾股定理可计算出OC=3,则CD=OC﹣OD=2,然后利用△CDE∽△CAD,根据相似比可计算出CE,再由AE=AC﹣CE可得AE的值.
试题解析:(1)证明:∵AB是⊙O的直径,∴∠ADB=90°,∴∠B+∠BAD=90°,∵AC为⊙O的切线,∴BA⊥AC,∴∠BAC=90°,即∠BAD+∠CAD=90°,∴∠B=∠CAD,∵OB=OD,∴∠B=∠ODB,而∠ODB=∠CDE,∴∠B=∠CDE,∴∠CAD=∠CDE,而∠ECD=∠DCA,∴△CDE∽△CAD;
(2)解:∵AB=2,∴OA=1,在Rt△AOC中,AC=![]() ,∴OC=
,∴OC=![]() =3,∴CD=OC﹣OD=3﹣1=2,∵△CDE∽△CAD,∴
=3,∴CD=OC﹣OD=3﹣1=2,∵△CDE∽△CAD,∴![]() ,即
,即![]() ,∴CE=
,∴CE=![]() ,∴AE=AC﹣CE=
,∴AE=AC﹣CE=![]() =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义运算
 =
=  ,若a≠﹣1,b≠﹣1,则下列等式中不正确的是( )
,若a≠﹣1,b≠﹣1,则下列等式中不正确的是( )
A. ×
×  =1
=1
B. +
+  =
= 
C.( )2=
)2= 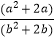
D. =1
=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】当a=3,b=-1时,求(a+b)(a-b)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.2x2x3=2x5
B.(x﹣2)2=x2﹣4
C.x2+x3=x5
D.(x3)4=x7 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(0,2),B(4,0).
(1)如图1,连接AB,若D(0,﹣6),DE⊥AB于点E,B、C关于y轴对称,M是线段DE上的一点,且DM=AB,连接AM,试判断线段AC与AM之间的位置和数量关系,并证明你的结论;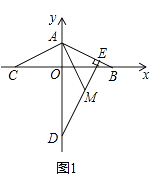
(2)如图2,在(1)的条件下,若N是线段DM上的一个动点,P是MA延长线上的一点,且DN=AP,连接PN交y轴于点Q,过点N作NH⊥y轴于点H,当N点在线段DM上运动时,△MQH的面积是否为定值?若是,请求出这个值;若不是,请说明理由.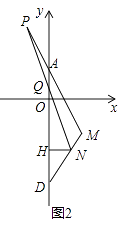
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程(m﹣1)x2+5x+m2﹣5m+4=0有一个根为0,则m的值等于( )
A. 1 B. 1或4 C. 4 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一元二次方程x2﹣6x+c=0有一个根为1,则c的值为_____.
相关试题

